部分群・剰余群 – Seto's Page

　このページでは部分群・剰余群の概念を、抽象的な話にならないよう具体的な点群や空間群を例に挙げて説明していきます。

部分群

　点群や空間群の説明のところで、群に何らかの対称操作を付け加え、次々と別の群を作り出していきました。作り出された新しい群には、もとの群の元がそのまま含まれています。一般に、ある群の部分集合が群の性質を満たすとき、それを部分群 (subgroup)といいます。一方、ある群を部分集合として含む全体集合が群の性質を満たすとき、それを超群 (supergroup)といいます。たとえば点群 $2$ は点群 $2/m$ の部分群ですし、点群 $2/m$ は点群 $2$ の超群です。要するに、群にも上下関係があるということです。

　部分群の概念は、結晶の相転移現象を理解する際に役に立ちます。なぜなら結晶が、何らかの外的要因の変化（例えば温度低下）に伴って相転移するとき、相転移前後の空間群が超群/部分群の関係になることがあるからです。このような相転移は、原子の位置がわずかに変化するような場合（変位型相転移）によくみられ、その結果双晶構造や反位相構造が形成されます。部分群の概念は、このような構造を解析する際の手がかりになります。

　部分群には、共役部分群や正規部分群と呼ばれるものがあります。簡単に説明します。

共役部分群と正規部分群

　群 $G$ とその部分群 $H$ があるとします。群 $G$ から元を一つ選び ($g$ とします)、部分群 $H$ の全ての元 (例えば $h_n$ ) に対して、$g^{-1}h_ng$ を計算してできる集合を、$H’ = g^{-1}H g$ と表現することにしましょう。このとき、$H’$も群$G$の部分群となるという性質があります。$H’$ と $H$ の関係を共役¹といい、$H’$ と $H$ は共役部分群 (conjugate subgtoup)である、といいます。さらに、群 $G$ の全ての元 ($g$) について $g^{-1}H g=H$ が成立するような場合（すなわち $g H = H g$ が成立する場合）、$H$ を正規部分群 (normal subgroup)といいます。分かりにくいですね。以下に具体例を示します。

　例えば点群 $4$ は以下の$h_0, h_1, g_0, g_1$ が元であり、$h_0, h_1$だけを選ぶと点群 $2$ になります。なお、$e$は単位行列(恒等変換)の意味です。
$$h_0=e=\begin{pmatrix}1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} ,\ \
h_1=\begin{pmatrix}-1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} ,\ \
g_0=\begin{pmatrix}0&1&0 \\ -1&0&0 \\ 0&0&1 \end{pmatrix} ,\ \
g_1=\begin{pmatrix}0&-1&0 \\ 1&0&0 \\ 0&0&1 \end{pmatrix}
$$このとき、$g_0^{-1} h_0 g_0 =h_0, \quad g_1^{-1} h_0 g_1= h_0, \quad g_0^{-1} h_1 g_0 = h_1, \quad g_1^{-1} h_1 g_1 =h_1$ という関係があります。したがって、点群 $2$ は点群 $4$ の正規部分群であるといえます。

　点群$3 2$ は、三回回転軸と、それに直交する二回回転軸が3本存在するという対称性です。以下のような6つの行列が元となります。$$
\begin{array}{lll}
t_0=e=\begin{pmatrix}1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} ,&
t_1=\begin{pmatrix}-\frac{1}{2}&-\frac{\sqrt{3}}{2}&0 \\ \frac{\sqrt{3}}{2} & -\frac{1}{2}&0 \\ 0&0&1 \end{pmatrix} ,&
t_2=\begin{pmatrix}-\frac{1}{2}&\frac{\sqrt{3}}{2}&0 \\ -\frac{\sqrt{3}}{2} & -\frac{1}{2}&0 \\ 0&0&1 \end{pmatrix},\\
a_0=\begin{pmatrix}1&0&0 \\ 0&-1&0 \\ 0&0&-1 \end{pmatrix} ,&
a_1=\begin{pmatrix}-\frac{1}{2}&\frac{\sqrt{3}}{2}&0 \\ \frac{\sqrt{3}}{2} & \frac{1}{2}&0 \\ 0&0&-1 \end{pmatrix} ,&
a_2=\begin{pmatrix}-\frac{1}{2}&-\frac{\sqrt{3}}{2}&0 \\ -\frac{\sqrt{3}}{2} & \frac{1}{2}&0 \\ 0&0&-1 \end{pmatrix}
\end{array}$$ $e$と$a_0$の集合は部分群です。同様に、$e$と$a_1$の集合、$e$と$a_2$ の集合も部分群です。それぞれを部分群 $A_0, A_1, A_2$ と呼ぶことにします。主軸の方向は異なりますが、どれも記号としては点群 $2$ です。ただし、$A_0, A_1, A_2$ は正規部分群ではありません。例えば $A_0$ ($e$と$a_0$の集合)について、 $ t_1^{-1} \ a_0 \ t_1 = a_1 $ となってしまうからです。だからと言って、$A_0, A_1, A_2$ が互いに無関係というわけでもありません。既に示したように $ t_1^{-1} \ a_0 \ t_1 = a_1 $ ですから、$ t_1^{-1} \ A_0 \ t_1 = A_1 $ であることが分かります。同様に、$ t_2^{-1} \ A_0 \ t_2 = A_2 $ となります。すなわち、$A_0, A_1, A_2$ は共役部分群の関係であるといえます。

　ところで、部分群が正規部分群であることが分かったら、どのような場面で役に立つのでしょうか。例えば実際の相転移に伴う微細組織（双晶や反位相構造）を観察したとして、「これは正規部分群に変化した結果である」などと判断することはおそらく困難です。正直に言って、実験や観察が主体の結晶学者にとって、即効薬になるような概念ではありません。正規部分群が力を発揮するのは、後述する剰余類を作るときです。正規部分群を法とすると左剰余類と右剰余類が等しくなるという性質があるからです。もとの点群や空間群から何らかの対称操作を差し引いたら、どのような群になるのかを考える際に役に立ちます。

剰余類・剰余群

　剰余類とは、ある群をその部分群で割り算(のようなことを)して分類したものです。剰余類同士は群を作り、剰余群と呼ばれます。こんな説明で分かったら苦労しませんよね。以下に、もう少し丁寧に説明します。

　$G$ を群とし、その正規部分群を $H$ とします。$G$ から2つの元 $g_1$ と $g_2$ を選んで $g_1^{-1} g_2$ を計算し、それが正規部分群 $H$ の元のどれか (仮に$h_n$) と一致したとき、「 $g_1$ と $g_2$ は同じ仲間(同値関係)である」と定義²しましょう。

ここで、$g_1^{-1} g_2 = h_n \Leftrightarrow g_2 = g_1 h_n$ という関係がありますから、$g_1$ とその仲間たちは、$g_1$に$h_1, h_2, h_3 \cdots$ のいずれかを掛けたものになるはずです。この集合を $g_1 H$ と表記すると、$$ g_1 H =\{g_1 h \ | \ h \in H\}$$と表すことが出来ます。群論では、この $g_1 H$ を「$g_1$ を含む剰余類」³といいます。

　具体例を見てみましょう。足し算を算法とする整数全体の集合(群)を$G$、3の倍数の集合(部分群)を$H$とします。$0$を含む剰余類は当然$H$そのものです。$$ 0 H = \{0+h \ | \ h \in H\}$$

1を含む剰余類はどうでしょうか。$ 1 H =\{1 + h \ | \ h \in H\}$ ということですから、要するに3で割って1余る整数の集合ということになります。同様に2を含む剰余類は、3で割って2余る整数の集合$ 2 H =\{2 + h \ | \ h \in H\}$となります。このようにして、整数全体の集合(群) $G$ は、$ 0 H (=H), 1 H, 2 H$ という三つの剰余類に分けることが出来ました。

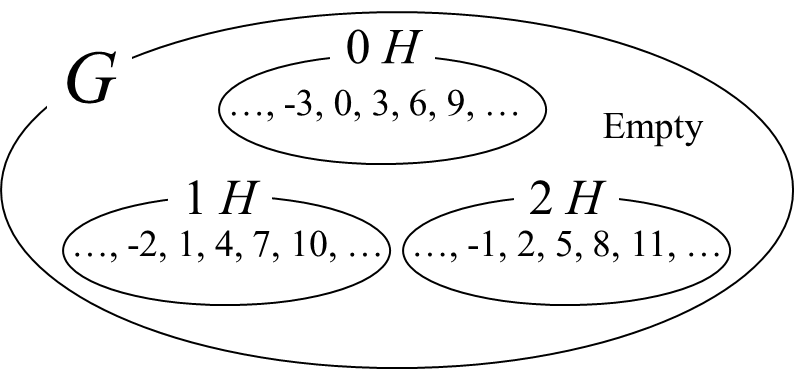
　ところで、三つの剰余類の内、群としての構造を持つのは $0 H$ のみです。$1 H$ と $2 H$ は群になりません⁴。ただし、$0 H, 1 H, 2 H$ を3つの元とみなして群を作ることは出来ます。すなわち、剰余類同士の算法を「それぞれの剰余類からひとつづつ任意に取り出した要素同士の足し算」と定義すれば、三つの剰余類$ 0 H, 1 H, 2 H$ は群となります。もちろん単位元は$0 H$ です。群論では、このような各剰余類を元とみなして作られる群を「3 (の倍数からなる部分群)を法とする剰余群」と表現します。記号としては、 $G/H$ のように表現します。

点群の剰余類・剰余群

　点群を使った剰余類の例を示しておきましょう。点群 $4/m$ は以下の8つの行列が元となります。$$
\begin{array}{l,l,l,l}
e=\begin{pmatrix}1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} ,&
s_1=\begin{pmatrix}-1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} ,&
s_2=\begin{pmatrix}0&1&0 \\ -1&0&0 \\ 0&0&1 \end{pmatrix} ,&
s_3=\begin{pmatrix}0&-1&0 \\ 1&0&0 \\ 0&0&1 \end{pmatrix}\\
s_4=\begin{pmatrix}1&0&0 \\ 0&1&0 \\ 0&0&-1 \end{pmatrix} ,&
s_5=\begin{pmatrix}-1&0&0 \\ 0&-1&0 \\ 0&0&-1 \end{pmatrix} ,&
s_6=\begin{pmatrix}0&1&0 \\ -1&0&0 \\ 0&0&-1 \end{pmatrix} ,&
s_7=\begin{pmatrix}0&-1&0 \\ 1&0&0 \\ 0&0&-1 \end{pmatrix}
\end{array}$$

この中から $e$ と $s_1$ を選ぶと正規部分群(点群 $2$ )になります。この部分群を $eH$ を呼びましょう。$eH$ の元に、たとえば $s_2$ を掛けると、$s_2 e = s_2, s_2 s_1 = s_3$ となり $s_3$ を掛けると $s_3 e = s_3, s_3 s_1 = s_2$ となりますから、 $s_2$ と $s_3$ は同じ剰余類であることが分かります。これを $s_2H$ と呼ぶことにしましょう。同様に、$s_4$ と $s_5$ 、$s_6$ と $s_7$ も同じ剰余類であり、それぞれ $s_4H, s_6H$ と呼びます。これらの剰余類の集合は「 $eH$ (=点群 $2$ )を法とする剰余群である」ということができます。

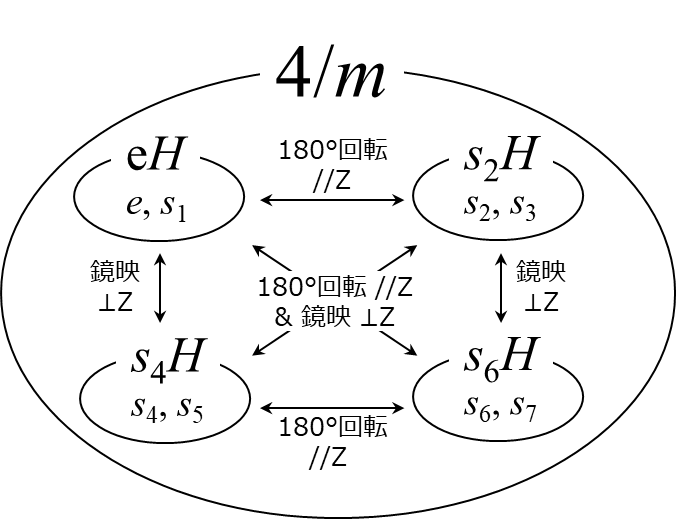
さて、この剰余群の構造を改めて眺めてみると、$eH$ と $s_2H$ の間には180°回転操作の関係があり、$s_4H$ と$s_6H$ も同様の関係があります。このほかにも、$eH$と$s_4H$ の間や$s_2H$と$s_6H$ の間に鏡映操作などが見つかります。もうお分かりですね、そうです、この剰余群は点群 $2/m$ の構造と同じになっているのです。要するに「点群 $4/m$ に対して部分群である点群 $2$ を法として剰余群をつくると、それは点群 $2/m$ と同値構造である」というわけです。厳密さは欠けますがより直感的な表現として「点群 $4/m$ から点群 $2$ の成分を除去すると点群 $2/m$ の性質が残る」、あるいは「点群 $4/m$ を点群 $2$ で割ると点群 $2/m$ になる」といい換えてもいいでしょう。剰余群の記法は $G/H$ のように書きますから、この場合は $(4/m)/(2)$となるわけです。割り算の記号がしっくりきますね。

空間群の剰余類・剰余群

　最後に、空間群の剰余について考えます。空間群 $Pnnn$ を例とします。この空間群は、以下のような8つの行列集合で表現することが出来ます。なお、$n_1, n_2, n_3$ は全ての整数を表します。また$e’$は単位行列そのものではなく、単位行列をふくむ行列の集合ですからプライム記号を付けています。他も同様です。
$$
e’=\begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3\\ 0&0&0&1\end{pmatrix}, \
s’_1=\begin{pmatrix}1&0&0&\frac{1}{2}+n_1\\ 0&1&0&\frac{1}{2}+n_2\\ 0&0&\bar{1}&n_3\\ 0&0&0&1\end{pmatrix},\
s’_2=\begin{pmatrix}\bar{1}&0&0&n_1\\ 0&1&0&\frac{1}{2}+n_2\\ 0&0&1&\frac{1}{2}+n_3\\ 0&0&0&1\end{pmatrix},\
s’_3=\begin{pmatrix}1&0&0&\frac{1}{2}+n_1\\ 0&\bar{1}&0&n_2\\ 0&0&1&\frac{1}{2}+n_3\\ 0&0&0&1\end{pmatrix} \\
s’_4=\begin{pmatrix}\bar{1}&0&0&\frac{1}{2}+n_1\\ 0&1&0&n_2\\ 0&0&\bar{1}&\frac{1}{2}+n_3\\ 0&0&0&1\end{pmatrix},\
s’_5=\begin{pmatrix}\bar{1}&0&n_1&\frac{1}{2}+n_2\\ 0&\bar{1}&0&\frac{1}{2}+n_3\\ 0&0&1&1\\ 0&0&0&1\end{pmatrix},\
s’_6=\begin{pmatrix}1&0&0&n_1\\ 0&\bar{1}&0&\frac{1}{2}+n_2\\ 0&0&\bar{1}&\frac{1}{2}+n_3\\ 0&0&0&1\end{pmatrix} ,\
s’_7=\begin{pmatrix}\bar{1}&0&0&n_1\\ 0&\bar{1}&0&n_2\\ 0&0&\bar{1}&n_3\\ 0&0&0&1\end{pmatrix}
$$ $e’$ はこの空間群の並進群であり正規部分群です。まずは $e’$ を法として剰余類を作ってみましょう。すぐにわかることですが、$s’_1$の中から任意の行列を選びそれを $e’$ の中のどの行列と作用させても、その結果は必ず $s’_1$ に含まれます。 $s’_2$ ~ $s’_7$ も同様です。すなわち上記の8つの行列集合は、最初から $e’$ を法とした剰余類になっていたということです。$e’$ は正規部分群ですから、当然8つの行列集合は群の構造をもちます。$e’$ が単位元です。念のため、この場合の算法は「それぞれの行列集合から1つずつ全ての組み合わせで行列を取り出しかけ合わせる」ということです。

　空間群 $Cc$ についても考えてみましょう。 $$
e’_0=\begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3 \\ 0&0&0&1\end{pmatrix},\ \
e’_1=\begin{pmatrix}1&0&0&n_1+\frac{1}{2}\\ 0&1&0&n_2+\frac{1}{2}\\ 0&0&1&n_3\\ 0&0&0&1\end{pmatrix},\ \
s’_2=\begin{pmatrix}1&0&0&n_1\\ 0&\bar{1}&0&n_2\\ 0&0&1&n_3+\frac{1}{2} \\ 0&0&0&1\end{pmatrix},\ \
s’_3=\begin{pmatrix}1&0&0&n_1+\frac{1}{2}\\ 0&\bar{1}&0&n_2+\frac{1}{2}\\ 0&0&1&n_3+\frac{1}{2}\\ 0&0&0&1\end{pmatrix} $$先ほどと同様に、並進群を法としましょう。ただし、この場合の並進群は $e’_0$ だけでなく$e’_1$ も含みます。$e’_0$ と $e’_1$ を合わせて並進群 ( $E$とします)となり、もちろん正規部分群でもあります。$E$ を法として剰余類を作ります。 $s’_2$ から任意の行列を選び、それを $E$ から選んだ行列と作用させると、その結果は $s’_2$ あるいは $s’_3$ の中のどれかと必ず一致します。 $s’_3$ の中から任意の行列を選び同じことをしても、やはりその結果は $s’_2$ あるいは $s’_3$ の中のどれかと一致します⁵。すなわち $s’_2$ と $s’_3$ (後半の二つ)は同じ剰余類ということになり、これと $E$ (前半の二つ)とをあわせて位数が2の剰余群が形成されます。

　あらためて、並進群を法として空間群を剰余した時の、各剰余類の関係を見てみましょう。いずれの例でも、左上の3行3列の部分行列($A$ とする) に注目すると、一切の重複がないことに気づくと思います。$$\begin{pmatrix}
A_{11} & A_{12} & A_{13} & B_x\\
A_{21} & A_{22} & A_{23} & B_y\\
A_{31} & A_{32} & A_{33} & B_z\\
0 & 0 & 0 & 1
\end{pmatrix}= \begin{pmatrix}
\begin{matrix} \\ \large{A} \\ \\ \end{matrix} & \begin{matrix} \\ \large{B} \\ \\ \end{matrix} \\
\begin{matrix}0&0&0\end{matrix} & 1
\end{pmatrix}
$$空間群 $Pnnn$ の場合はもともと $A$ の部分の重複はありませんでしたし、空間群 $Cc$ の場合は $A$ の部分が同一の行列集合がまとまってひとつの剰余類になりました。並進群を法として剰余すると、かならずこのような性質が生まれます⁶。アフィン変換行列の場合、$A$ の部分は $A$ の部分にしか影響を及ぼしませんから、結局このような剰余類の関係は $A$ の部分だけを取り出した群の構造と同値ということです。そして$A$ の部分は、並進を伴わない対称操作 (回転、回反、対称心、鏡映) を表すということを思い出してください。つまり、空間群の部分群である並進群を法として剰余群を作ると、それは点群と同じ代数的構造を持っている、ということになります⁷。これがずばり空間群と点群の群論的関係です。正確さには欠けますが、より直感的な表現として「空間群から $A$ の部分だけ取り出した集合が点群である」といってもよいかもしれません。上記の場合、空間群 $Pnnn$ は点群 $mmm$ と、空間群 $Cc$ は点群 $m$ と同じ構造です。

脚注

線形代数を学ぶとたびたび出くわすのが、この「共役」という用語です。元 $A, B$ があったとして、 $A^{-1}\ B\ A$ という量はどういう意味をもつのでしょうか。 $A, B$ を具体的に何かの座標 ($X$) を変換する行列と考えてみましょう。$A^{-1}\ B\ A\ X$ という量を、①まず $X’=A\ X$ を計算し、②次に $X” = B\ X’$ を計算し、③最後に$A^{-1}\ X”$を計算して得た結果と考えましょう。この一連の作業は、①’ $A$ で別の座標系に変換し、②’ $B$ を作用させた後、③’ $A^{-1}$ によって元の座標系に戻すと解釈することもできるはずです。つまり、左右を挟んでいる $A^{-1}$ と$A$ は、「 $B$ という作用の座標系を変換させる役割」である、と考えるとすっきりするでしょう。たとえば $A$ が $X$軸と一致する-90°回転操作であり、$B, C$ がそれぞれ $Y, Z$軸と一致する90°回転操作であったとしたら、$$
A=\begin{pmatrix}1&0&0\\0&0&1\\0&-1&0\end{pmatrix}, \
B=\begin{pmatrix}0&0&1\\0&1&0\\-1&0&0\end{pmatrix}, \
C =\begin{pmatrix}0&-1&0\\1&0&0\\0&0&1\end{pmatrix}= A^{-1}\ B\ A
$$このような関係を見出せますから、「 $B$ と $C$ ($=A^{-1}BA$) は $A$ (という座標変換)によって共役(な関係)である」、と表現します。
　さらに蛇足ですが、複素数の世界では、$a, b$ を任意の実数として、$a+ bi$ と$a-bi$ は共役であるといったりします。これは複素平面で虚数を反転させるという座標変換に関して共役であるいう意味です。算法は足し算でもかけ算でも構いません。実際に確認してみましょう。ある複素数 ($c+ di$とします)の虚数部を反転($c-di$になる)したあと、算法が足し算とかけ算のケースで場合分けです。
・足し算の場合: $a+bi$を足して $a+c+(b-d)i$ となり、再び虚数部分を反転すると $a+c-(b-d)i$ を得る。これは$a-bi$と$c+ di$を足したものと等しい。
・かけ算の場合: $a+bi$をかけて $ac-bd-(ad-bc)i$ となり、再び虚数部を反転すると $ac-bd+(ad-bc)i$ を得る。これは$a-bi$と$c+ di$をかけたものと等しい。
したがって、算法が足し算だろうとかけ算だろうと $a+ bi$ と$a-bi$ は虚数の反転操作に関して共役です。 ↩︎
同値関係をもう少し厳密に説明します。2つの元の間で何らかの比較方法が定義され、その方法の下で $x$ と $y$ が等しいということを $x\sim y$と表すとします。この関係が、① $x\sim x$ (反射律)、② $x\sim y$ ならば $y\sim x$ (対称律)、③ $x\sim y$ かつ $y\sim z$ ならば $x\sim z$ (推移律) という三つの条件を満たした時、$\sim$を同値関係といいます。例えば、「3で割って余りを比べる」という比較方法 (すなわち mod 3の世界)の場合は、 $4\sim1$とか $16\sim-2$と表せるわけです。私たちが小学生のころから使っている等号記号 $=$ も、数式や数値の同値関係を表す記号です。 ↩︎
もちろん正確に言うとこれは左剰余群です。Hに正規部分群を選んだ場合、左剰余群と右剰余群は等しい($g H = H g$)ので左右を区別する必要ありません。 ↩︎
そもそも$1H$や$2H$は単位元を含んでいませんし、$1$と$4$は$1H$の元だが $1+4=5$は$2 H$の元になったりして、演算も成立しません。 ↩︎
$E$ は正規部分群なので、わざわざ $s’_3$ について確認しなくてもよいのですが、あえて冗長に書きました。 ↩︎
ある空間群について並進群を法として剰余したら、 $A$ の部分が全く同じ剰余類が生まれたと仮定します。$A$ の部分が同じであれば、それらの関係は単なる平行移動(並進)ですから、互いを変換する操作は並進群に含まれるはずです。ところが、並進群を法とする剰余群において、並進群は単位元としてふるまいます。単位元によってある剰余類を別の剰余類に変換することはできません。すなわち最初の仮定は間違っており、$A$ の部分の重複は有り得ないということになります。 ↩︎
空間群がらせん操作と映進操作の両方とも含んでいない場合は、剰余群としてではなく、単なる部分群として点群を含むと考えることもできます。 ↩︎