結晶族点群とは
点群は無数に存在します。例えば回転操作を元に含むような点群であれば、回転角度を適当に変えることでいくらでも新しいものを作り出すことが出来ます。ところが、対象を結晶に限定した場合、回転角度は自由に設定することは出来ません。結晶は単位格子並進によって空間を埋め尽くす必要があるため、許される回転(回反)角度は、0°, 60°, 90°, 120°, 180°, 240°, 270°, 300°のいずれかであることが要請されます。この要請は、「回転あるいは回反の次数は 1, 2, 3, 4, 6 に限定される」という表現と等価です。次数が 1, 2, 3, 4, 6 の回転あるいは回反操作1を、いろいろと向きを変えながら組み合わせて群を作ると、全部で32種類しか生み出されません。この32種類を、結晶族点群といいます2。
結晶族点群の部分群
以下に、32種類の結晶族点群について、部分群・超群の関係を示します。
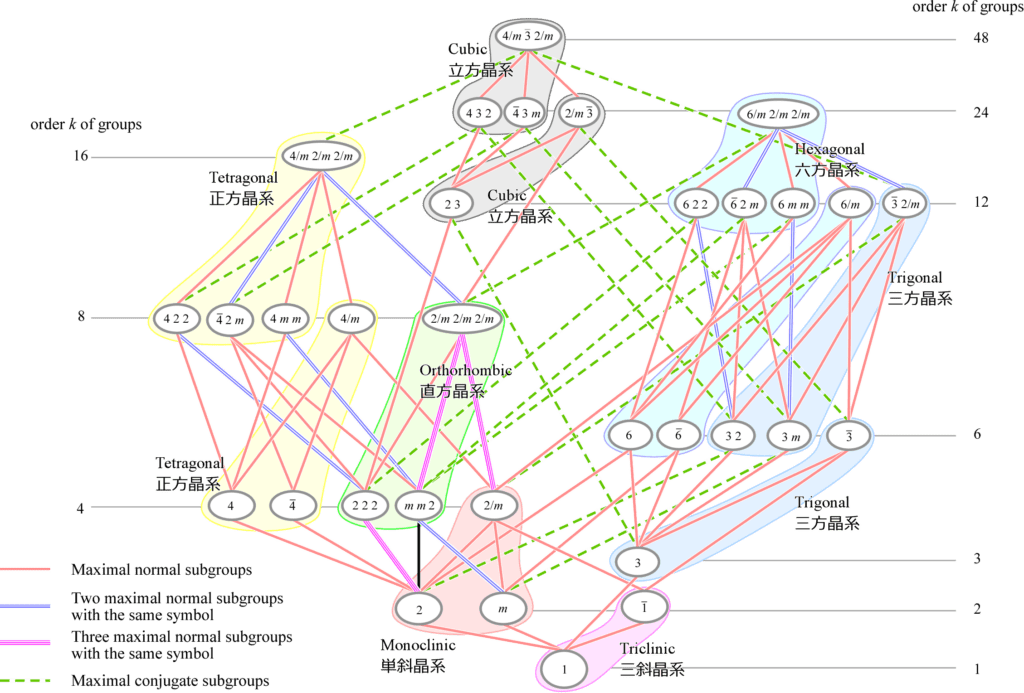
すべての結晶族点群の中で点群 \(1\) は最下部に位置し、その位数は1です。単位行列だけからなる点群です。一方、点群 \(4/m\ \bar{3} \ 2/m\) は最も対称性の高い点群であり、その位数は48です。ただし、点群 \(4/m\ \bar{3} \ 2/m\) がすべての点群の超群になるというわけではありません。点群 \(6/m\ 2/m\ 2/m\) を局所的な頂点とする六方晶系の点群たちは、どのような対称操作を加えても点群 \(4/m\ \bar{3} \ 2/m\) を含む立方晶系の点群たちへたどり着けません。立方晶系に属する点群と六方晶系も属する点群との間には、超群/部分群の関係はないのです。一方、三方晶系は、立方晶系と六方晶系のどちらの部分群にもなり得ます。このあたりの事情は、別ページの解説をご覧ください。以下、図中の用語解説です。
- order k of groups: 位数、すなわち群が含む元(操作)の数です。一般点が写される数と考えてもよいです。
- normal subgroup: 正規部分群のことです。線が2本あるいは3本の場合は、方向の異なる部分群が2つあるいは3つ存在するということを意味します。例えば点群 \(222\) からは、3つの異なる方向の部分群(ただし記号としてはすべて点群 \(2\)) を取り出すことができます。
- conjugate subgroup: 共役部分群のことです。共役というくらいですから当然共役な関係にある複数の部分群(ただし記号は同じ)が存在します。例えば点群 \(32\) の共役部分群は 3つの異なる方向の点群\(2\)です。
- Maximal subgroup: 極大部分群といいます。自分自身を除いて元の数が極大になるような部分群のことです。複数存在することがあります。たとえば点群\(6\) の極大部分群は点群\(3\) と点群\(2\) です。詳しい説明はこちらをご覧ください。
例: \(4/m\)の部分群
点群 \(4/m\) の 8 個の対称操作を元とする群です。対称操作をザイツ記号3で表現して乗積表4を書き下すと以下のようになります。
| \(1\) | \(2_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) | |
| \(1\) | \(1\) | \(2_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) |
| \(2_{001}\) | \(2_{001}\) | \(1\) | \(4^-_{001}\) | \(4^+_{001}\) | \(\bar{1}\) | \(m_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) |
| \(4^+_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(2_{001}\) | \(1\) | \(\bar{4}^-_{001}\) | \(\bar{4}^-_{001}\) | \(m_{001}\) | \(\bar{1}\) |
| \(4^-_{001}\) | \(4^-_{001}\) | \(4^+_{001}\) | \(1\) | \(2_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{1}\) | \(m_{001}\) |
| \(m_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(1\) | \(2_{001}\) | \(4^-_{001}\) | \(4^+_{001}\) |
| \(\bar{1}\) | \(\bar{1}\) | \(m_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(2_{001}\) | \(1\) | \(4^+_{001}\) | \(4^-_{001}\) |
| \(\bar{4}^+_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(4^-_{001}\) | \(4^+_{001}\) | \(2_{001}\) | \(1\) |
| \(\bar{4}^-_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{1}\) | \(m_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(1\) | \(2_{001}\) |
上の乗積表から、群としての要件を満たしつつ、なるべく多くの元を選んでみましょう。まず、以下のように赤く囲った操作(元)を選び出して作られる群が、点群 \(4\)です。
| \(1\) | \(2_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) | |
| \(1\) | \(1\) | \(2_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) |
| \(2_{001}\) | \(2_{001}\) | \(1\) | \(4^-_{001}\) | \(4^+_{001}\) | \(\bar{1}\) | \(m_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) |
| \(4^+_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(2_{001}\) | \(1\) | \(\bar{4}^-_{001}\) | \(\bar{4}^-_{001}\) | \(m_{001}\) | \(\bar{1}\) |
| \(4^-_{001}\) | \(4^-_{001}\) | \(4^+_{001}\) | \(1\) | \(2_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{1}\) | \(m_{001}\) |
| \(m_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(1\) | \(2_{001}\) | \(4^-_{001}\) | \(4^+_{001}\) |
| \(\bar{1}\) | \(\bar{1}\) | \(m_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(2_{001}\) | \(1\) | \(4^+_{001}\) | \(4^-_{001}\) |
| \(\bar{4}^+_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(4^-_{001}\) | \(4^+_{001}\) | \(2_{001}\) | \(1\) |
| \(\bar{4}^-_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{1}\) | \(m_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(1\) | \(2_{001}\) |
以下のように赤く囲った操作(元)を選び出して作られる群が、点群 \(\bar{4}\)です。
| \(1\) | \(2_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) | |
| \(1\) | \(1\) | \(2_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) |
| \(2_{001}\) | \(2_{001}\) | \(1\) | \(4^-_{001}\) | \(4^+_{001}\) | \(\bar{1}\) | \(m_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) |
| \(4^+_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(2_{001}\) | \(1\) | \(\bar{4}^-_{001}\) | \(\bar{4}^-_{001}\) | \(m_{001}\) | \(\bar{1}\) |
| \(4^-_{001}\) | \(4^-_{001}\) | \(4^+_{001}\) | \(1\) | \(2_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{1}\) | \(m_{001}\) |
| \(m_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(1\) | \(2_{001}\) | \(4^-_{001}\) | \(4^+_{001}\) |
| \(\bar{1}\) | \(\bar{1}\) | \(m_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(2_{001}\) | \(1\) | \(4^+_{001}\) | \(4^-_{001}\) |
| \(\bar{4}^+_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(4^-_{001}\) | \(4^+_{001}\) | \(2_{001}\) | \(1\) |
| \(\bar{4}^-_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{1}\) | \(m_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(1\) | \(2_{001}\) |
以下のように赤く囲った操作(元)を選び出して作られる群が、点群 \(2/m\)です。
| \(1\) | \(2_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) | |
| \(1\) | \(1\) | \(2_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) |
| \(2_{001}\) | \(2_{001}\) | \(1\) | \(4^-_{001}\) | \(4^+_{001}\) | \(\bar{1}\) | \(m_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) |
| \(4^+_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(2_{001}\) | \(1\) | \(\bar{4}^-_{001}\) | \(\bar{4}^-_{001}\) | \(m_{001}\) | \(\bar{1}\) |
| \(4^-_{001}\) | \(4^-_{001}\) | \(4^+_{001}\) | \(1\) | \(2_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{1}\) | \(m_{001}\) |
| \(m_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(1\) | \(2_{001}\) | \(4^-_{001}\) | \(4^+_{001}\) |
| \(\bar{1}\) | \(\bar{1}\) | \(m_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(2_{001}\) | \(1\) | \(4^+_{001}\) | \(4^-_{001}\) |
| \(\bar{4}^+_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{4}^-_{001}\) | \(m_{001}\) | \(\bar{1}\) | \(4^-_{001}\) | \(4^+_{001}\) | \(2_{001}\) | \(1\) |
| \(\bar{4}^-_{001}\) | \(\bar{4}^-_{001}\) | \(\bar{4}^+_{001}\) | \(\bar{1}\) | \(m_{001}\) | \(4^+_{001}\) | \(4^-_{001}\) | \(1\) | \(2_{001}\) |
なお、\(4/m\) にとって\(4, \bar{4}, 2/m\) は全て正規部分群ですから剰余群をつくることができます5。\(4/m\) に対して、\(4\) を法とした剰余群は \(m\) となり、\(\bar{4}\) を法とした剰余群は \(\bar{1}\) となり、\(2/m\) を法とした剰余群は \(2\) となります。
例: 点群 \(2\ 2\ 2\) の部分群
点群 \(2\ 2\ 2\) の構造は以下のような乗積表で表現できます。
| \(1\) | \(2_{100}\) | \(2_{010}\) | \(2_{001}\) | |
| \(1\) | \(1\) | \(2_{100}\) | \(2_{010}\) | \(2_{001}\) |
| \(2_{100}\) | \(2_{100}\) | \(1\) | \(2_{001}\) | \(2_{010}\) |
| \(2_{010}\) | \(2_{010}\) | \(2_{001}\) | \(1\) | \(2_{100}\) |
| \(2_{001}\) | \(2_{001}\) | \(2_{010}\) | \(2_{100}\) | \(1\) |
上の乗積表から群としての要件を満たすように部分群を選び出すやり方には、以下の三通りがあります。
| \(1\) | \(2_{100}\) | \(2_{010}\) | \(2_{001}\) | |
| \(1\) | \(1\) | \(2_{100}\) | \(2_{010}\) | \(2_{001}\) |
| \(2_{100}\) | \(2_{100}\) | \(1\) | \(2_{001}\) | \(2_{010}\) |
| \(2_{010}\) | \(2_{010}\) | \(2_{001}\) | \(1\) | \(2_{100}\) |
| \(2_{001}\) | \(2_{001}\) | \(2_{010}\) | \(2_{100}\) | \(1\) |
| \(1\) | \(2_{100}\) | \(2_{010}\) | \(2_{001}\) | |
| \(1\) | \(1\) | \(2_{100}\) | \(2_{010}\) | \(2_{001}\) |
| \(2_{100}\) | \(2_{100}\) | \(1\) | \(2_{001}\) | \(2_{010}\) |
| \(2_{010}\) | \(2_{010}\) | \(2_{001}\) | \(1\) | \(2_{100}\) |
| \(2_{001}\) | \(2_{001}\) | \(2_{010}\) | \(2_{100}\) | \(1\) |
| \(1\) | \(2_{100}\) | \(2_{010}\) | \(2_{001}\) | |
| \(1\) | \(1\) | \(2_{100}\) | \(2_{010}\) | \(2_{001}\) |
| \(2_{100}\) | \(2_{100}\) | \(1\) | \(2_{001}\) | \(2_{010}\) |
| \(2_{010}\) | \(2_{010}\) | \(2_{001}\) | \(1\) | \(2_{100}\) |
| \(2_{001}\) | \(2_{001}\) | \(2_{010}\) | \(2_{100}\) | \(1\) |
これらは全て表記としては 「点群 \(2\) 」なのですが、2回回転軸の方向は異なります。つまり、\(222\)の極大部分群は方位の異なる三つの \(2\) ということになります。このページで最初に示した図では、このような状況が3本の線で表現されています。