三方晶系と六方晶系の区別
「三方晶系」と「六方晶系」はどちらも \(a=b,\,\, \alpha=\beta=90°,\,\, \gamma=120°\) という六方格子設定 (Hexagonal lattice setting) の単位格子で表現できる晶系です。 両者を区別する基準は、点群や空間群の記号中に \(3\) が出てくるか、\(6\) が出てくるか、ということではありません。例えば点群 \(\bar{6}\) は六方晶系です。\(\bar{6}\) ( \(6\) 回回反)という操作は\(3/m\) ( \(3\) 回回転と鏡面)という操作と等価ですが、\(3/m\)と表記したとしても三方晶系に含めてはいけません。
三方晶系と六方晶系の区別の本質は、菱面格子設定 (Rhombohedral lattice setting) をとれるかどうか、ということです。これだけで理解できる人は大変優秀ですので、以降の説明は読み飛ばしてください。なお、このページで用いる「六方格子設定」あるいは「菱面格子設定」という用語は単に格子の幾何学的形状を表しています。「3.7. 空間群の分類」ページで説明する「格子系」の概念とは少し異なりますのでご注意ください。
三方晶系と六方晶系には以下の 12 種の点群があります。そのすべてについて、「底面が正六角形の直角柱」の面の模様を塗り分けることで対称性を表現できます。実際に塗り分けた図形を以下に示します。
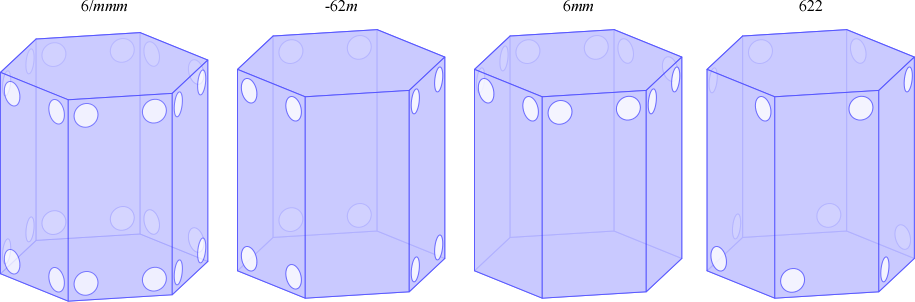
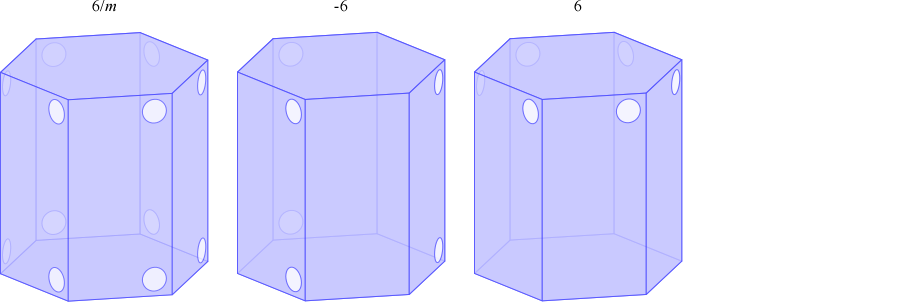
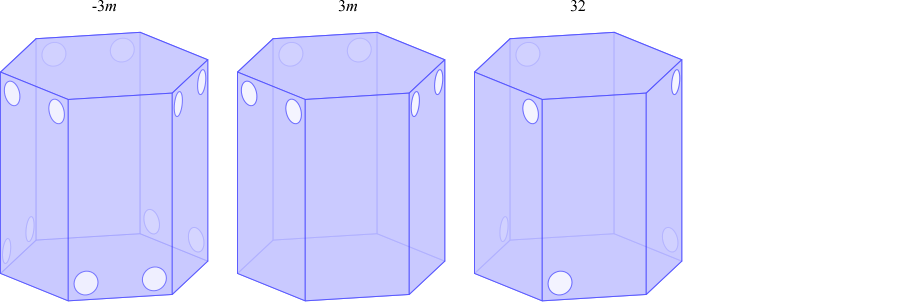
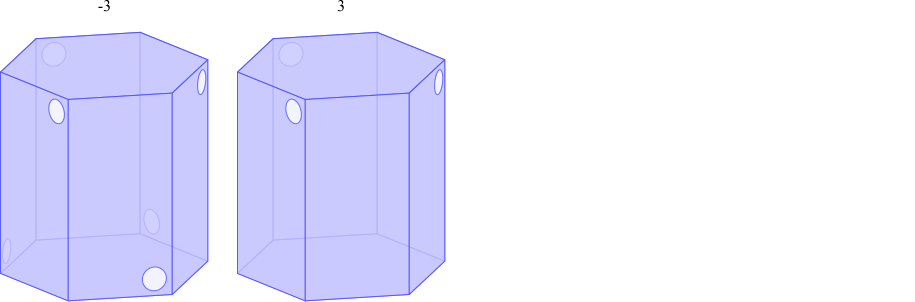
「底面が正六角形の直角柱」を3分割すると、以下のように底面が菱形の直角柱が得られます。単位格子表現でいえば \(a=b, \alpha=\beta=90°, \gamma=120°\) (六方格子設定)です。
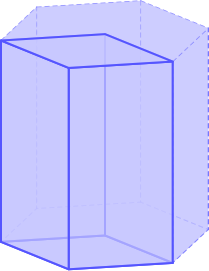
点群に並進操作を加えたものが空間群ですから、三方晶系と六方晶系に属する結晶はすべて上のような六方格子設定の単位格子を持つことができます。
三方晶系に属する点群は、上記の立体に加えて、「立方体を、一つの体対角線方向に引き伸ばした(あるいは押し縮めた)形状」(菱面体)でもその対称性を表現することができます。実際に塗り分けた図形を以下に示します。
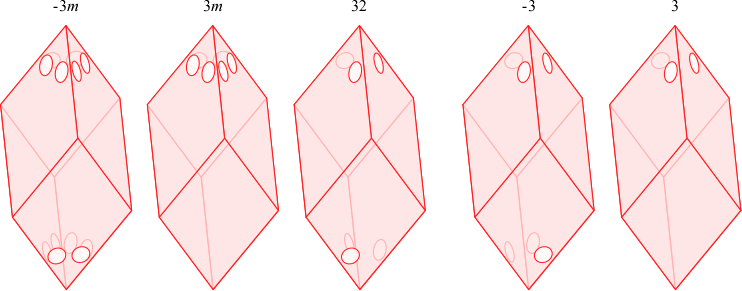
この菱面体は単位格子表現でいえば\(a=b=c,\,\, \alpha=\beta=\gamma\) (菱面格子設定)です。三方晶系の結晶は、六方格子設定だけでなく菱面格子設定の単位格子を持つこともできるわけです。一方、菱面体の各面をどのように塗り分けたとしても、六方晶系に属する点群の対称性を表現することはできません。当然、六方晶系に属する結晶が菱面格子設定の単位格子を持つことも有り得ません。
以上をまとめます。三方晶系の結晶にとって、意味のある単位格子は稜面格子設定か六方格子設定のいずれかです。六方晶系の結晶にとって意味のある単位格子は六方格子設定のみです。(補足: 「意味のある」というのは、単位格子が格子並進以外の対称操作を反映した形状をもつ、ということです)
群論的な表現をすれば、「立方晶系の部分群になりうるのが三方晶系で、なり得ないのが六方晶系である」 ということもできます。詳しくは、「2.5. 結晶族点群とその部分群」をご覧ください。また、三方晶系と六方晶系でなぜこのようなややこしい状況になってしまうのかという背景については、「3.7. 空間群の分類」を参考にしてください。
ちなみに、「三方晶系であれば \(3\) 回回転軸が存在する」は正解なのですが、「六方晶系であれば \(6\) 回回転軸が存在する」は間違いです。例えば、点群 \(\bar{6}\) や \(\bar{6}2m\) は、6回回転軸を持ちません。\(\bar{6}\)(6回回反)は \(3/m\) と等価であることを忘れないようにしましょう。
六方格子設定 と 菱面格子設定
上で述べたように、三方晶系に属する結晶は六方格子設定 (\(a=b,\,\, \alpha=\beta=90°,\,\, \gamma=120°\)) か菱面格子設定 (\(a=b=c,\,\, \alpha=\beta=\gamma\))か、どちらかの形状の単位格子を持つことができます。両者の関係を考察しましょう。
3回回転軸を持つ結晶を考えます。結晶ですから、3つの独立した並進ベクトルがあるはずです。並進ベクトルの始点(格子点)をどこに置くかは人間様の自由ですので、ここでは3回回転軸上に格子点(灰色の丸)を置くところからスタートします。

ここで一つ仮定を置きます。「3回回転軸と垂直でも平行でもない方向に、短い並進ベクトルがある」という仮定です1。このベクトルおよび格子点を水色で示しました。
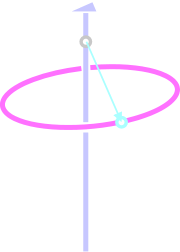
水色の格子点は、3回回転軸の作用によってクリーム色と黄緑色に映ります。三本のベクトルを単位格子ベクトル \(a, b, c\) と考えれば、「\(a=b=c,\,\, \alpha=\beta=\gamma\)」という菱面格子設定になることがわかりますね。これで単位格子の出来上がり、と考えてもよいのですがもう少し話を進めます。
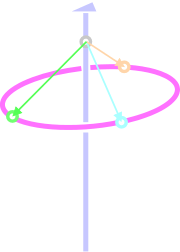
この3つのベクトル (水色、クリーム色、黄緑色) を合成すると、そのベクトルの終点は3回回転軸上に位置します。すなわち、3回回転軸上にも格子点が存在するわけです。
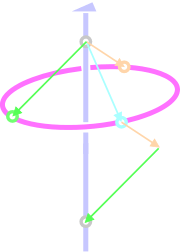
格子点と格子点を結べば、それは必ず並進ベクトルです。3回回転軸上の格子点を結ぶベクトルも当然並進ベクトルです。これを青いベクトルで示しましょう。また、3回回転軸と直交するような2本のベクトル(赤と緑)を選ぶこともできます。これも並進ベクトルです。赤、緑、青の並進ベクトルを \(a, b, c\) 軸と考えれば、「\(a=b,\,\, \alpha=\beta=90°,\,\, \gamma=120°\)」という六方格子設定の単位格子の出来上がりです。
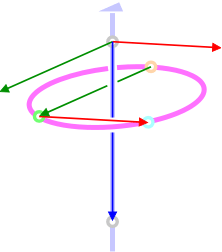
ところで、この単位格子は、最小体積の単位格子(=Primitiveな単位格子)ではありません。例えば \(c\) 軸(青)方向に1/3だけ進んだ \(c\) 軸断面では、下の図のように、水色の格子点が単位格子の中に入っています。水色の格子点の分率座標は、(2/3, 1/3, 1/3)です。同様に、 \(c\) 軸方向に2/3だけ進んだ \(c\) 軸断面では(1/3, 2/3, 2/3)の場所に格子点が見つかります。
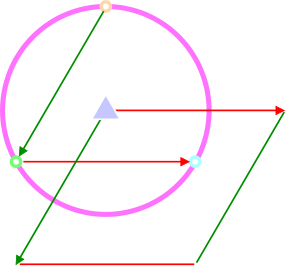
ここまでの話をまとめると、「3回回転軸と垂直でも平行でもない方向に短い並進ベクトル」があったとしても、結局は六方格子(\(a=b,\,\, \alpha=\beta=90°,\,\, \gamma=120°\))の形状の単位格子を取れてしまう、ただし、余分な格子点を単位格子内に二つ含む、ということです。もうお分かりですね。そうです、これが、 \(R\) 格子タイプの空間群における六方格子設定というやつです。例えば \(R3\) という空間群の結晶を六方格子設定で表現したければ、\(a\) 軸と \(c\) 軸の長さを指定し、(2/3, 1/3, 1/3)と(1/3, 2/3, 2/3)の格子並進を考慮する必要があります。一方、途中で出てきた菱面格子(\(a=b=c,\,\, \alpha=\beta=\gamma\))形状の単位格子が \(R\) 格子の空間群における菱面格子設定です。例えば \(R3\) の結晶を菱面格子設定で表現したければ、\(a\) 軸の長さと \(\alpha\) の角度を指定します。この菱面格子設定は単純単位格子(最小体積の単位格子)の表現ですから、内部に余計な格子点を含みません。それならば記号 \(P\) (Primitive)を使ってほしいところですが、そうすると別の混乱が生じます。もう少し話を進めます。
今度は「3回回転軸と垂直でも平行でもない方向に短い並進ベクトル」が存在しない場合を考えてみましょう。これは簡単です。要するに「3回回転軸と垂直あるいは平行な短い並進ベクトルがある」ということですから、それらの並進ベクトルをそのまま \(a, b, c\) 軸として六方格子をとることが出ます。当然この単位格子は単純単位格子(\(P\)格子)です。例えば \(P3, P32, P3m\) みたいな空間群がこのケースに該当します。\(P\) の記号はこれらが使ってしまっているので、 菱面格子設定の空間群でたとえ単純単位格子だったとしても \(P\) の記号を使うことは出来ません。
ところで、\(P3, P32, P3m\) のような空間群でも、六方格子の \(a, b, c\) 軸ベクトルを適切に組み合わせれば(例えば \(a+c, b+c, -a-b+c \) の三つを単位格子ベクトルとすれば)、菱面格子設定すなわち「\(a=b=c,\,\,\alpha=\beta=\gamma\)」を満たすような単純単位格子を採用することもできます。ただし、そんなことは普通はしません。なぜなら、菱面格子設定を採用すると \(3\) 回回転軸に垂直あるいは平行な結晶面や晶帯軸の表現が直感的に分かりにくくなってしまうから、あるいはたいていの人間にとって菱面格子設定より六方格子設定の方が理解しやすいから、です。(もっと深い理由があるかもしれません。詳しい方のご意見をお待ちしております。)
最後に全体をまとめます。結晶が \(3\) 回回転軸を有していれば、必ず六方格子設定の単位格子をとることが出来ます2。その六方格子設定が単純単位格子であれば \(P\) 格子タイプ、そうでなければ \(R\) 格子タイプと表現することが国際ルールで決められています。\(R\) 格子タイプの空間群に関しては、単純単位格子である稜面格子設定を採用してもよいことになっています。
六方格子設定におけるの結晶面/軸の四指数表現
ミラー・ブラヴェ指数
結晶面は、通常\((h\, k\, l)\) のように三つの指数 \(h, k, l\)で表現します。これをミラー指数 (Miller index) といいます3。しかし、三方あるいは六方晶系に対して六方格子設定 (Hexagonal setting) を採用した場合に限って、結晶面を \((h\, k\, i\, l)\)のように四つの指数で表現すると便利なことがあります。これをミラー・ブラヴェ指数 (Miller-Bravais index) といいます4。
三方あるいは六方晶系の六方格子設定では \(c\)軸が3回回転軸と一致します。この3回回転操作で結ばれる等価な結晶面の集合を考えてみましょう。三指数表現の場合、例えば\((1\, 2\, 1)\)と等価な結晶面は \((\bar{3}\, 1\, 1)\)と\((2\, \bar{3}\, 1)\)なのですが、この3枚の面指数を見て即座に等価であると判断するのはちょっと難しいですよね。
結晶面の四指数表現\((h\, k\, i\, l)\)では、\(i=-h-k\)となるように\(i\)を定めます。たとえば三指数の\((1\, 2\, 1)\)は、四指数では\((1\, 2\, \bar{3}\, 1)\)と表現します。そしてこの結晶面は3回回転操作によって \((\bar{3}\, 1\, 2\, 1)\), \((2\, \bar{3}\, 1\, 1)\) に写ります。これらの指数をみると \(h, k, i\) が循環可換(cyclically permutable)、すなわち\((h\, k\, i\, l)\) ⇔ \((i\, h\, k\, l)\) ⇔ \((k\, i\, h\, l)\) の関係を持つことが分かります。要するに、四指数表現\((h\, k\, i\, l)\) にすれば3回回転で結ばれる等価な結晶面を見分けやすい、ということです。 はい、便利ですね。変換の仕方も簡単で覚えやすいため、広く普及しています。
ウェバー指数
さて、六方格子設定において結晶面の四指数表現が便利ならば、結晶軸の四指数表現も便利なのでは、と思われたことでしょう。そうです、軸の四指数表現もあります。これをウェバー指数 (Weber index)5といいます。通常、軸の方向は三指数で\([u\, v\, w]\) と表現しますが、三方/六方の六方格子設定に限っては \([\frac{2u-v}{3}\,\frac{2v-u}{3}\,\frac{-u-v}{3}\,w]\)というウェバー指数で表現することも出来ます。逆に四指数で \([u’\,\, v’\,\, i’\,\, w’]\) と書かれていたら、三指数へは \([2u’+v’\,\, u’+2v’\,\, w’]\) と変換してください。たとえば、三指数表現で\([1\, 2\, 1]\), \([\bar{2}\, \bar{1}\, 1]\), \([1\, \bar{1}\, 1]\) は等価なんですが、一見すると等価かどうか分かりにくいですね。これを四指数表現にすると \([0\, 1\, \bar{1}\, 1]\), \([\bar{1}\, 0\, 1\, 1]\), \([1\, \bar{1}\, 0\, 1]\)となります。たしかに循環可換な関係になっていて等価な結晶軸を見分けやすくなっています。また、\(w=0\)の時に限って、\([u\, v\, i\, 0]\)軸は\((u\, v\, i\, 0)\)面の法線方向と一致するという性質もあります。
| 三指数表現 | 四指数表現 | |
|---|---|---|
| 結晶面 | \((h\, k\, l)\) | \((h\, k\, i\, l)\) ただし \(i=-h-k\) |
| 結晶軸 | \([u\, v\, w]\) | \(\displaystyle\left[\frac{2u-v}{3}\,\frac{2v-u}{3}\,\frac{-u-v}{3}\,w\right]\) |
| \([2u’+v’\,\, u’+2v’\,\, w’]\) | \([u’\,\, v’\,\, i’\,\, w’]\) ただし \(i’=-u’-v’\) |
ところで、結晶面の四指数表現は広く使われていますが、結晶軸の四指数表現は一部の業界を除いてあまり普及していません。おそらく、変換式が分かりにくいこと、ワイスの晶帯則( \(hu+kv+lw=0\)ならば\((h\, k\, l)\)面の法線と\([u\, v\, w]\)軸は直交するという規則)が使えなくなること、そもそも結晶面ではなく結晶軸が主役になるような解析の場面が少ないこと、などが理由です。このあたりの事情に興味のある方はネスポロ先生の論文もお読みください。
\(P321\)と\(P312\)
点群32に属する空間群のなかに、\(P321\) と \(P312\) があります。なぜこの二つを分ける必要があるのか、不思議に感じたことは無いでしょうか。点群 \(321\) と点群 \(312\) は全く同じ代数的構造を有していますから、点群のみの議論で十分な場合 (並進性を考慮しなくてよい場合) は、両者を区別する必要はありません。ところが並進操作を有する空間群の場合、並進方向と回転軸方向の関係を考慮する必要があり、\(P321\)と\(P312\) は別物になってしまうのです。以下に詳しく説明します。
まず、\(P321\)と\(P312\) は共に「 \(3\) 回回転軸と、それに直交する \(2\) 回回転軸が存在する」という空間群です。3次元空間群ですから当然 3 方向の並進操作 (並進ベクトル) も含むわけですが、「 \(3\) 回回転軸が存在する」という条件のみから、並進ベクトルの1つは \(3\) 回回転軸と平行、残り2つは \(3\) 回回転軸に直交、というふうに選ぶことが出来ます (「六方格子設定と菱面格子設定」を参照のこと)。この \(3\) 回回転軸に直交する2つの並進ベクトルを、\(a, b\) と呼ぶことにします。
さて、この空間群には \(3\) 回回転軸に加えてそれと直交する \(2\) 回回転軸もあるのでした。当然 \(2\) 回回転軸は \(3\) 回回転の要請によって 3 方向 (正負を区別すれば 6 方向) 存在します。 これらの \(2\) 回回転軸と並進ベクトル \(a, b\) は、どのような方位関係を持ちうるでしょうか。でたらめな方位関係では空間群として成立しなくなってしまうので、答えは限定されます。証明は省きますが、以下のニ通りの関係に絞られます。
ケース①: 2回回転軸が \(a\) や \(b\) の方向と一致
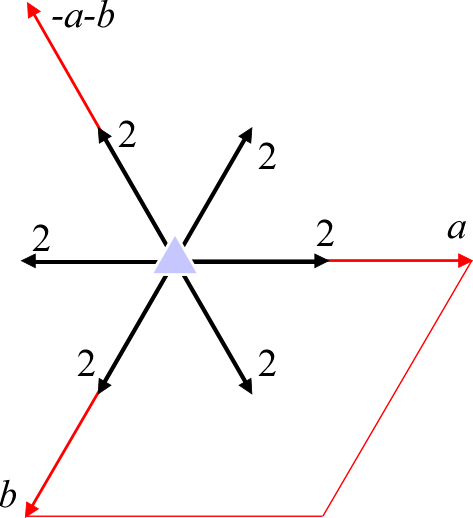
ケース②: 2回回転軸が \(a-b\) や \(a+2b\) の方向と一致
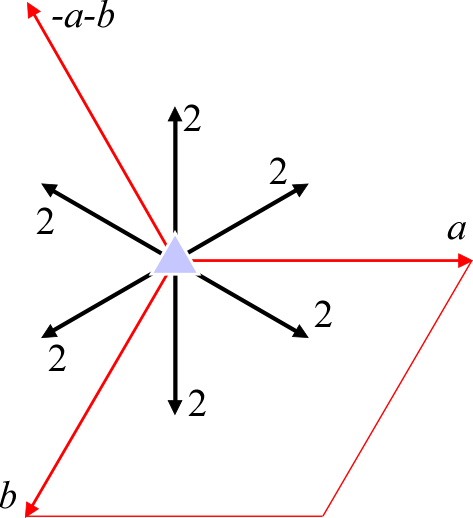
上図は \(3\) 回回転軸 ( \(c\) 軸) の方向から投影したものです。もうお分かりですね、要するにケース①が \(P321\) に、ケース②が \(P312\) に対応するということなのです。以下にこの2つの空間群の対称操作および一般点の関係を示します。全く違う空間群であることが分かると思います。
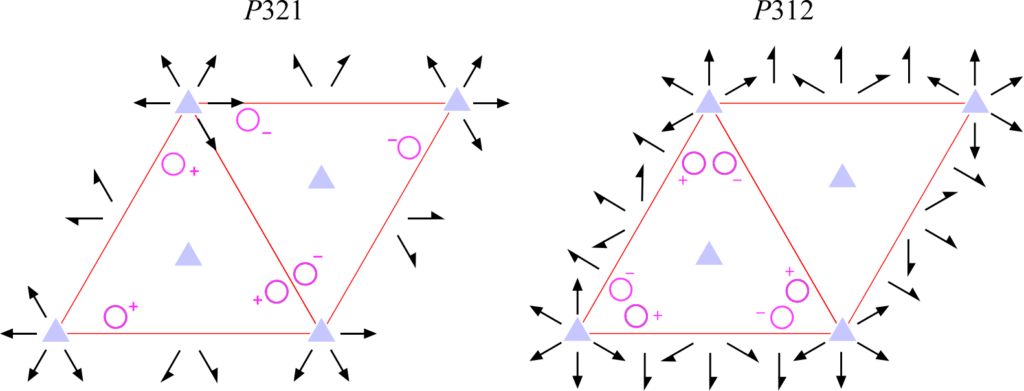
ここでは \(P321\) と \(P312\) を例に挙げて説明しましたが、同様の関係は、
- \(P3_121\) と \(P3_112\)
- \(P3_221\) と \(P3_212\)
- \(P3m1\) と \(P31m\)
- \(P3c1\) と \(P31c\)
- \(P\bar{3}m1\) と \(P\bar{3}1m\)
- \(P\bar{3}c1\) と \(P\bar{3}1c\)
にも当てはまります。表記が似ているからと言って取り間違えないように気を付けましょう。
なお、実はこのような関係は正方晶系にも見られます。例えば、点群 \(\bar{4}2m\) に属する空間群における \(P\bar{4} 2m\) と \(P\bar{4} m2\) 、\(P\bar{4} 2c\) と \(P\bar{4} c2\) 、\(I\bar{4} 2m\) と \(I\bar{4} m2\) などの関係です。これらは上記で述べたような並進ベクトルとの方位関係によって区別されています。
ところで、\(P312\) のような ケース②の空間群の物質の物性を取り扱う際は、点群やラウエクラスとの関係に注意しましょう。例えば、弾性率や誘電率などのテンソルはラウエクラスによってその形状が決まりますが、多くの文献では①の形式でのみ解析が行われています。ケース①の形式で解析された弾性率をケース②のタイプの結晶に適用する際には、\(a-b → a’\), \(a+2b → b’\) のような軸変換を行う必要があります。
- 「3回回転軸と垂直でも平行でもない方向に短い並進ベクトル」という表現の中の「短い」の意味は、正確に言うと \(c\) 軸に垂直な成分が小さいかどうか、ということです。もっとも \(c\) 軸垂直な成分が小さいベクトルは \(c\) 軸に平行なベクトルです。他の独立なベクトルの、\(c\) 軸垂直な成分が最も短いものを選んだ時、そのベクトルの \(c\) 軸平行な成分がゼロであれば \(P\) 格子、ゼロでなければ \(R\) 格子ということになります。 ↩︎
- 他の回転や回反の次数でも同様の考察を展開すると、「次数が2以上の回転・回反操作を有する場合、一本の並進ベクトルが残り二本の並進ベクトルと直交するような設定(すなわち直角柱形状の単位格子)が可能である」という結論が得られます。 ↩︎
- W. H. Miller (1839), A treatise on crystallography, Cambridge. https://commons.wikimedia.org/wiki/Category:A_Treatise_on_Crystallography_(1839)_by_MILLER ↩︎
- 文献によっては、ブラヴェ・ミラー指数と書かれている場合もあります。 ↩︎
- L. Weber (1922) Das viergliedrige Zonensymbol des hexagonalen Systems. Z. Kristallogr. 57, 200–203. ↩︎