空間群は230種類あります。これらは互いに無関係なわけではなく、共通の性質に注目して分類する(まとめる)ことができます。結晶系やブラベー格子などの概念も空間群の分類方法ですが、これまでの説明はやや不正確あるいは不十分なところがありました。ここでは、改めてよく使われる空間群の分類法のいくつかを詳しく解説します。大きな分類 (項目数が多い)から小さな分類(項目数が少ない)の順に話を進めていきます。
空間群と空間群タイプ
これまでこのHPではなんども「空間群は230種類ある」のように書いてきましたが、実はこれは不正確な表現です。正しくは「空間群タイプは230種類ある」です。空間群は必ず並進操作を含み、その並進量や並進方向は結晶によって異なります。例えばNaClとMgOはどちらも\(Fm\bar{3}m\)という空間群の対称性を持ちますが、格子定数は異なる (前者は a=5.64Å、後者は a=4.21Å) ので表記が同じだったとしても異なる対称操作を持った空間群に属すると考えなければいけません。つまり空間群は無限に存在するのです。
一方、格子定数の違いを無視して空間群を代数的な構造で整理すると、230種類の空間群タイプ (space group types) が得られます。ところでおそらく多くの方にとって、「格子定数の違いを無視」して空間群を議論することはほぼ自明の前提であるとお考えでしょう。そのためこのHPでは、正確さはわずかに犠牲にしますが誤解が生じない範囲で、空間群タイプのことを単に空間群と呼ぶ1ことにします。
アフィン空間群
「2.4. 群の乗積表・同型」ページで述べたように、230種類の3次元空間群のうち、以下の11のペアは互いに同型です。
- 正方晶系: \(P4_1\)と\(P4_3\)、\(P4_122\)と\(P4_322\)、\(P4_12_12\)と\(P4_32_12\)
- 三方晶系: \(P3_1\)と\(P3_2\)、\(P3_121\)と\(P3_221\)、\(P3_112\)と\(P3_212\)
- 六方晶系: \(P6_1\)と\(P6_5\)、\(P6_2\)と\(P6_4\)、\(P6_122\)と\(P6_522\)、\(P6_222\)と\(P6_422\)
- 立方晶系: \(P4_132\)と\(P4_332\)
各ペアは 鏡像異形 (enantiomorphic) の関係を持っています。これら11ペアの同型重複を同一とみなした 219 種類の空間群をアフィン空間群 (affine space-group types) といいます。一方、同型重複を独立と数えた230種類を真アフィン空間群(proper affine space-group types) あるいは結晶空間群 (crystallographic space-group types)といいます。通常、空間群といえば後者の方を指します。
結晶類と結晶族点群
「2.3. 部分群・剰余群の概念」ページで述べたように、すべての空間群について並進群を法とした剰余群を導いたとき、それらは32種類の結晶族点群 (並進操作と両立する回転・回反を組み合わせた点群)のいずれかに対応します。このように空間群を点群に対応させる分類を結晶類2 (crystal class) あるいは幾何学的 (geometric) 結晶類 といいます。結晶類と結晶族点群は一対一で対応し表記も全く一緒ですが、概念は微妙に異なることにご注意ください。前者は空間群に対応する点群を指しており、後者は点群そのものです。
一般に結晶類は結晶のマクロな性質に深く関連します。なぜなら、結晶類は巨視的な結晶の外形を形態学的対称性に従って群に分類したものに対応するからです。例えば結晶の外形や各種物性 (弾性率、熱伝導率、透磁率など) は結晶類で表現される点群の対称性に従います。
ある空間群がどの結晶類に属しているかは、実は次のような簡単な記号の置き換えや削除によって知ることができます。すなわち空間群表記 (HM表記) から
- 最初の一文字 (格子の記号) を削除
- すべての下付き数字 (らせん軸の並進情報) を削除
- すべての小文字アルファベット (映進操作) を \(m\) に変換
すればよいのです。例えば空間群 \(Fd\bar{3}m\) の結晶類は \(m\bar{3}m\)であり、空間群 \(P6_422\) の結晶類は \(622\) となります。
代数的結晶類と共型空間群
単に結晶類といったら、上述の幾何学的結晶類を指します。実はもう一つ似た言葉として、代数的結晶類 (arithmetic crystal class) があります。代数的結晶類とは、(幾何学的)結晶類にブラベー格子を組み合わせた概念です。結晶類が32種類であったのに対し代数的結晶類は73種類あります。代数的結晶類は共型空間群 (symmorphic space groups) と一対一の対応関係があります。共型空間群とは、らせんと映進の対称操作を含まず、点群操作と格子並進操作のみを組み合わせてできる空間群のことです。例えば空間群 \(Fm\bar{3}m\) は共型空間群のひとつですが、 \(I4_1acd\) は共型空間群ではありません。
ブラベー格子とブラベー代数的類
既に別ページでも説明していますが、ブラベー格子 (Bravais lattice, Bravais type of lattice3) とは、単純格子の頂点にのみ原子が存在するような結晶を仮定し格子の形状をいろいろ変化させると、何種類の空間群で表現できるか?という発想に基づく分類です。以下に14種類のブラベー格子を再掲し、さらにそれらに対応する空間群(格子を並べた全体の対称性)と点群 (一つの格子点を不動にする対称性) を記載します。
| 記号 | 模式図 | 空間群 | 点群 |
|---|---|---|---|
| \(aP\) | 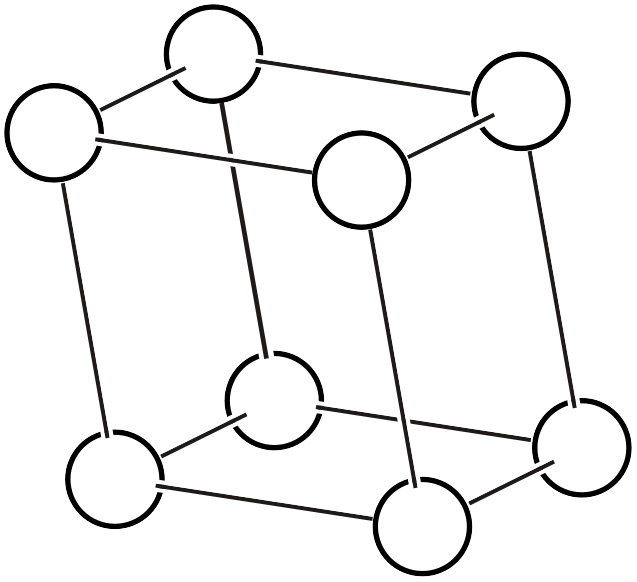 | \(P\bar{1}\) | \(\bar{1}\) |
| \(mP\) | 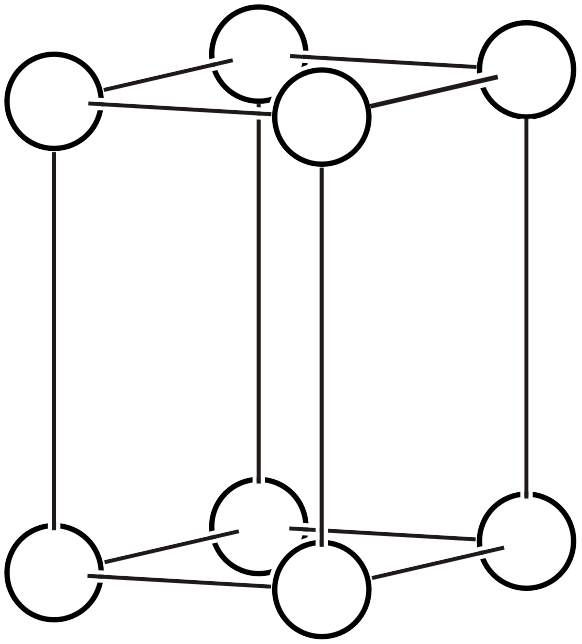 | \(P2/m\) | \(2/m\) |
| \(mC\) | 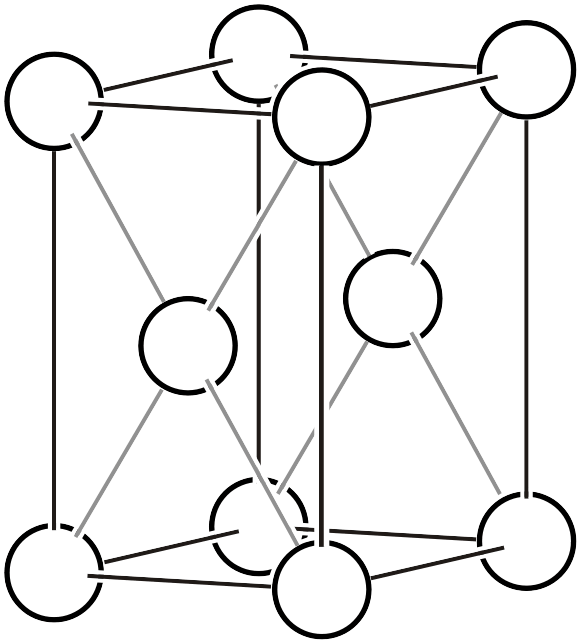 | \(C2/m\) |
| 記号 | 模式図 | 空間群 | 点群 |
|---|---|---|---|
| \(oP\) | 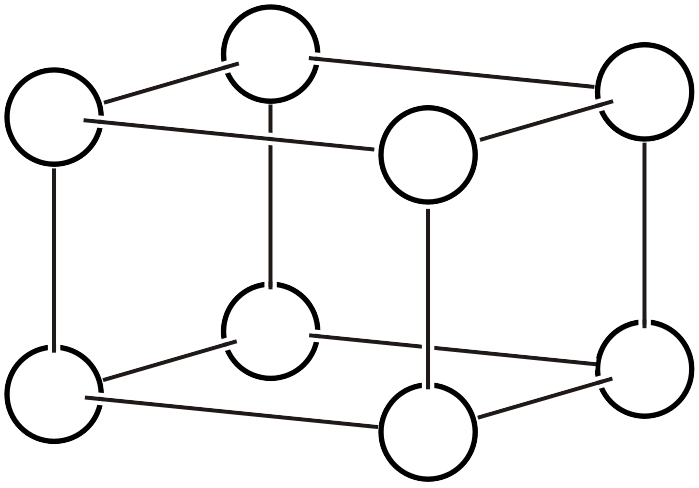 | \(Pmmm\) | \(mmm\) |
| \(oC\) | 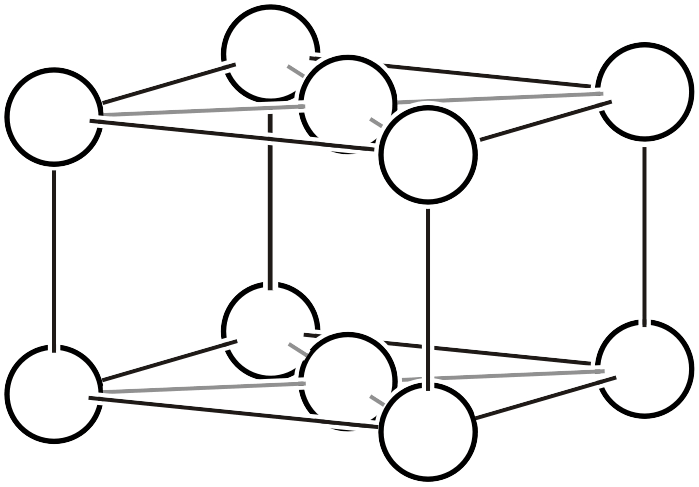 | \(Cmmm\) | |
| \(oI\) | 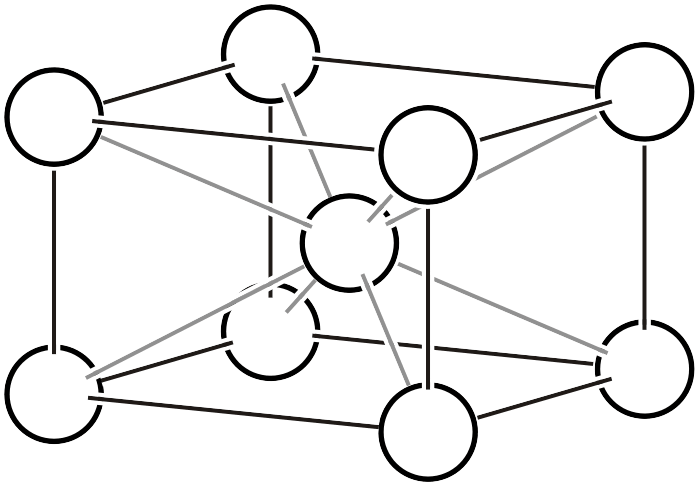 | \(Immm\) | |
| \(oF\) | 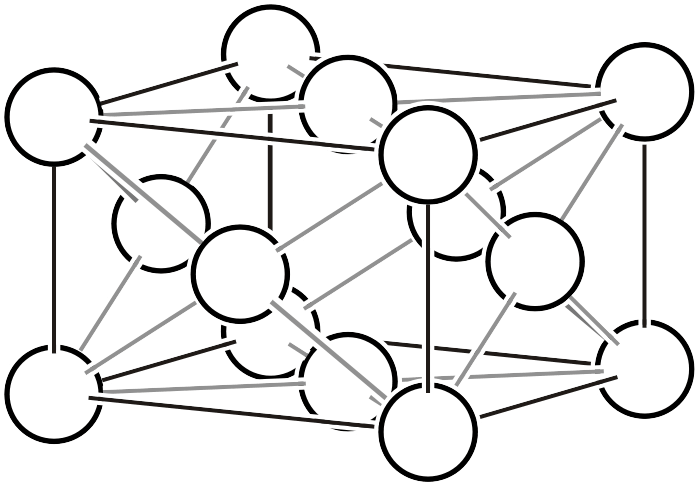 | \(Fmmm\) | |
| \(tP\) | 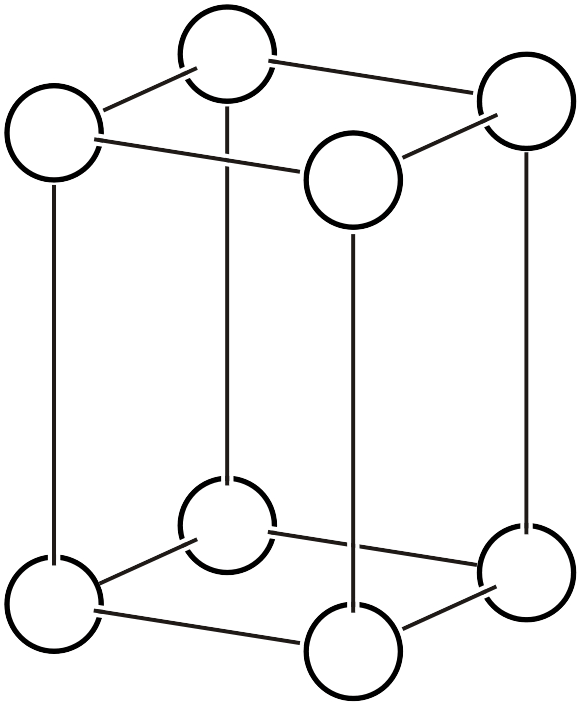 | \(P4/mmm\) | \(4/mmm\) |
| \(tI\) | 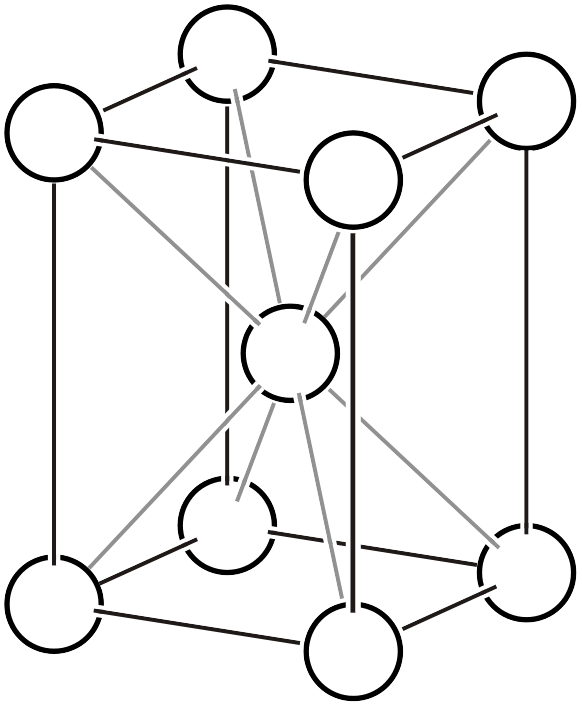 | \(I4/mmm\) |
| 記号 | 模式図 | 空間群 | 点群 |
|---|---|---|---|
| \(hR\) | 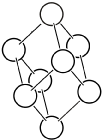 | \(R\bar{3}m\) | \(\bar{3}m\) |
| \(hP\) | 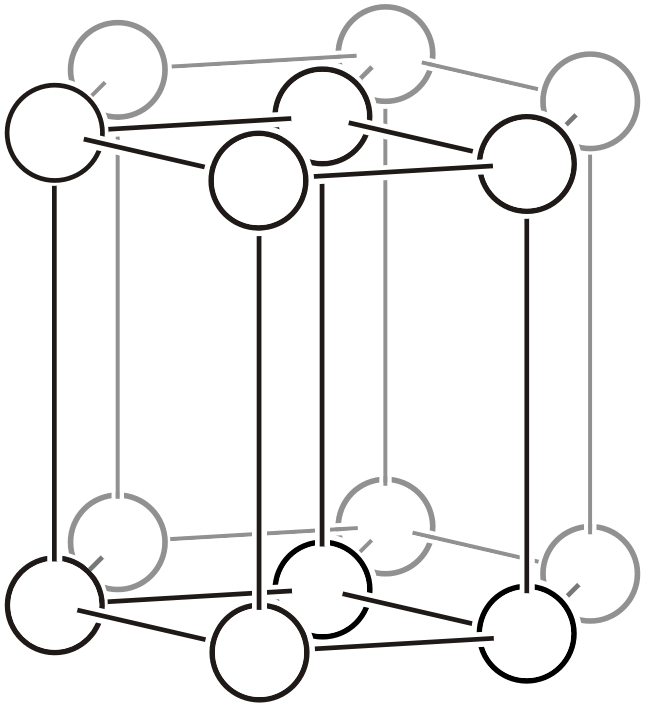 | \(P6/mmm\) | \(6/mmm\) |
| \(cP\) | 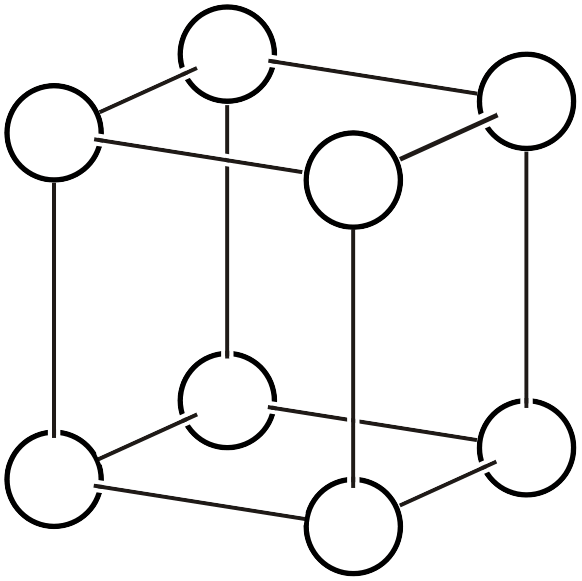 | \(Pm\bar{3}m\) | \(m\bar{3}m\) |
| \(cI\) | 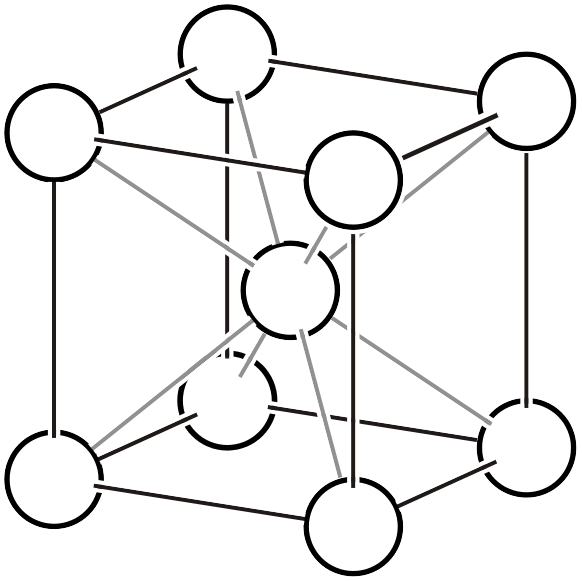 | \(Im\bar{3}m\) | |
| \(cF\) | 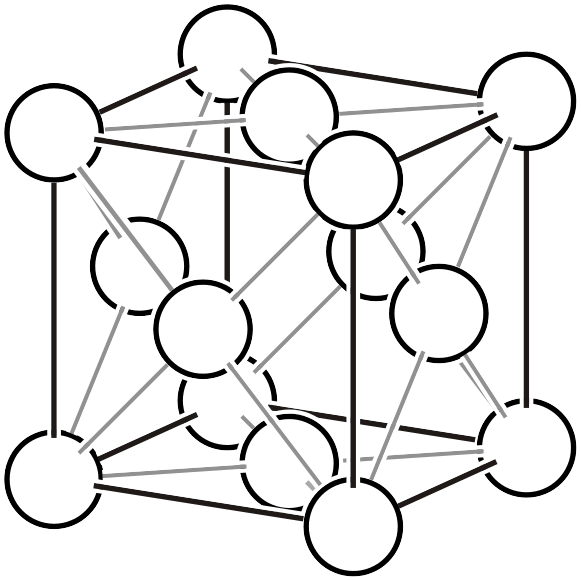 | \(Fm\bar{3}m\) |
単純格子を仮定したのに、なぜ複合格子が生まれるのか?という疑問を持たれたかもしれません。「格子定数・結晶系・ブラベー格子」ページでも説明しているとおり、複合格子は単純格子に分解できますので、逆に絶妙な形の単純格子を仮定すれば複合格子を生み出すことができるのです。
実際の結晶は単位胞の頂点以外の場所にも原子が存在していますが、空間群の並進対称要素にだけ注目すれば、すべての結晶は上記の14種類のいずれかに必ず分類できます。このような分類をブラベー代数的類 (Bravais arithmetic class) あるいは単にブラベー類といいます。ブラベー格子(タイプ)とブラベー代数的類は一対一で対応します。ただし両者の混同を避けるため、ブラベー代数的類は空間群表記中の格子記号を最後にして、さらに底心格子記号を\(S\)と変換して、例えば \(mmmI\) (空間群\(Immm\)に対応)とか \(2/mS\)(空間群\(C2/m\)に対応) と書く決まりになっています。
格子系・結晶系・結晶族
これらはかなり混乱しやすい用語です。そんなに困っている人はいないかもしれませんが、念のため説明しておきます。
格子系
全ての結晶は14種類のブラベー代数的類 (≒ブラベー格子) に分類できます。そして、対応する点群に注目してブラベー代数的類をさらに分類したものが格子系 (lattice system) です。ブラベー格子中のひとつの格子点に注目して、それを不動にする対称操作がつくる点群4は、次のように7 種類にまとめることができます。この基準でブラベー代数的類を分類したものを格子系といいます。
| 格子系 (lattice system) | 点群 | 対応するブラベー格子 |
|---|---|---|
| 三斜格子系 (triclinic) | \(\bar{1}\) | \(aP\) |
| 単斜格子系 (monoclinic) | \(2/m\) | \(mP\), \(mC\) |
| 直方格子系 (orthorhombic) | \(mmm\) | \(oP\), \(oC\), \(oI\), \(oF\) |
| 正方格子系 (tetragonal) | \(4/mmm\) | \(tP\), \(tI\) |
| 菱面格子系 (rhombohedral) | \(\bar{3}m\) | \(hR\) |
| 六方格子系 (hexagonal) | \(6/mmm\) | \(hP\) |
| 立方格子系 (cubic) | \(m\bar{3}m\) | \(cP\), \(cI\), \(cF\) |
六方格子系を除く格子系は単位胞の形状の対称性がそのまま点群に対応しています5。だからといって格子系は単位胞形状の対称性によって分類されていると考えるのは間違いです。この考え方だと六方格子系 (点群 \(6/mmm\)) の単位胞の対称性6を説明できません。「格子」とは、ひとつの単位胞 (平行六面体の箱)ではなく、格子点の相対的位置関係を表現する格子模様だということを思い出しましょう。格子系とは、あくまで格子模様の対称性(点群)による分類であることにご注意ください。
結晶系
全ての結晶は、32種類の(幾何学的)結晶類 (≒結晶族点群) に分類できます。そして以下のように結晶類をさらに分類したものが結晶系 (crystal system) です。
| 結晶系 (crystal system) | 所属する結晶類 (点群) | ユニークな対称要素 |
|---|---|---|
| 三斜晶系 (triclinic) | \(1\), \(\bar{1}\) | \(1\) あるいは \(\bar{1}\) |
| 単斜晶系 (monoclinic) | \(2\), \(m\), \(2/m\) | \(2\)あるいは\(m\) |
| 直方晶系 (orthorhombic) | \(222\), \(mm2\), \(mmm\) | 3方向に\(2\)あるいは\(m\) |
| 正方晶系 (tetragonal) | \(4\), \(\bar{4}\), \(4/m\), \(422\), \(\bar{4}2m\), \(4/mmm\) | \(4\) あるいは \(\bar{4}\) |
| 三方晶系 (trigonal) | \(3\), \(\bar{3}\), \(32\), \(3m\), \(\bar{3}m\) | \(3\) あるいは \(\bar{3}\) |
| 六方晶系 (hexagonal) | \(6\), \(\bar{6}\), \(6/m\), \(622\), \(6mm\), \(\bar{6}m2\), \(6/mmm\) | \(6\) あるいは \(\bar{6}\) |
| 立方晶系 (cubic) | \(23\), \(m\bar{3}\), \(432\), \(\bar{4}3m\), \(m\bar{3}m\) | 四方向に\(3\) |
結晶系は格子系に比べて広く普及している分類法ですが、実はこの分類に深い数学的背景があるわけではありません。結晶系のひとつめの分類方針は、32の結晶類(に対応する点群)が有する様々な対称要素から共通性を見出して分類する、という方針です。例えば、3方向に\(2\)あるいは\(m\)という対称要素を持つ三つの点群 \(222\), \(mm2\), \(mmm\) は一つにまとめる、みたいな感じです。なぜ「3方向」に限定するのか?1方向だけでもいいことにして、\(2\), \(m\), \(2/m\)も仲間に入れてあげたら?と思う人がいるかもしれません。これはもっともな疑問です。そこでもう一つ、なるべく格子系の分類に近づける7、という方針を加えてみましょう。すなわち、同じ格子系に属する空間群たちが、なるべく同じ結晶系に属するような対称要素の共通性を考えるということです。ふたつ目の方針を考慮すると、上の表のように7つの結晶系が導かれるのです。
この分類は一見きれいにみえますが、重要な注意点があります。三方晶系はふたつ目の方針を満たしていないのです。三方晶系に属する空間群は、六方格子系になることも菱面格子系になることもありますが、結晶類は同じです (例えば空間群\(P3\)と\(R3\)は、格子系ではそれぞれ六方と菱面だが、結晶類では共に\(3\)となり区別は不可能)。この意味で、三方晶系とは六方格子系にも菱面格子系にもなりうる結晶類をまとめたものであり、六方晶系とは必ず六方格子系になる結晶類をまとめたものである、と考えるとスッキリするかもしれません8。このあたりの事情は「三方/六方晶系の話題」ページでも詳しく解説しています。三方晶系と六方晶系を除く残り5つの結晶系 (三斜、単斜、直方、正方、立方) は、同一名称の格子系と完全な対応関係があります(例えば立方晶系に属する空間群は必ず立方格子に属します)。
結晶族
格子系と結晶系の概念が理解できたら、結晶族 (Crystal family) の概念の理解は容易です。要するに、格子系と結晶系の公約数であり、格子系と結晶系とで食い違いのあった部分を「六方晶族」としてまとめた分類です。以下に、結晶族、格子系、結晶系の関係をまとめます。
| 結晶族 | 格子系 | 結晶系 | ブラベー格子の数 | 点群の数 | 空間群の数 |
|---|---|---|---|---|---|
| 三斜 | 1 | 2 | 2 | ||
| 単斜 | 2 | 3 | 13 | ||
| 直方 | 4 | 3 | 59 | ||
| 正方 | 2 | 7 | 68 | ||
| 六方 | 菱面 | 三方 | 1 | 5 | 7 |
| 六方 | 1 | 18 | |||
| 六方 | 7 | 27 | |||
| 立方 | 3 | 5 | 36 | ||
とくに注意が必要なのは六方晶族ですね。この晶族には、「菱面格子系の三方晶系」、「六方格子系の三方晶系」、「六方格子系の六方晶系」という三種類の空間群が所属しています。ややこしいですね。「三方晶族」とか「菱面晶系」とか「三方格子(系)」という分類は存在しないので、うっかり口走らないように注意しましょう。ほかの結晶族は、同じ名称の格子系および結晶系と完全対応するので、悩む必要はありません。
まとめ
最後に、このページで紹介した空間群の分類の階層構造をまとめます。この図はITA (6th ed)のFig. 1.3.4.1を改変したものです。
最上位には230種の空間群が位置します。正確に言うと空間群タイプです。空間群から同型重複をまとめると、219種のアフィン空間群に分類されます。アフィン空間群のらせん操作と映進操作をそれぞれ回転操作と鏡映操作に変換すると、73種の代数的結晶類 (≒共型空間群) が得られます。
代数的結晶類は、並進操作に注目すれば14種のブラベー代数的類 (≒ブラベー格子)に分類され、さらに格子点の対称性から7種の格子系に分類されます。あるいは代数的結晶類は、点群要素に注目すれば32種の幾何学的結晶類 (≒結晶族点群) に分類され、さらに共通の対称要素を括りだすことで7種の結晶系に分類されます。
格子系と結晶系の最大公約数を取った分類が6種の結晶族です。
脚注
- 実際、ほとんどの日本語の教科書では、「空間群」と「空間群タイプ」を区別せず用いているように思います。厳密にいえば、結晶の温度が1℃でも異なれば、熱膨張によって体積(つまり格子定数)が変化するので、空間群タイプは同じでも空間群は変化します。でも、いくら何でもこんな厳密な言葉遣いは面倒ですよね。 ↩︎
- crystal class を「晶族」 と訳す場合もあります。ただこのように訳すと、今度は crystal familyをどう訳せばいいかという問題が生じます。このHPでは crystal class は結晶類で統一します。https://dictionary.iucr.org/Crystal_class ↩︎
- IUCRの勧告によれば、ブラベー格子は個別の格子そのものではなく格子の種類を表す概念なので、Bravais type of lattice と表現することが勧められています。日本語でもブラベー格子タイプと表現した方がいいのかもしれませんが、上記の空間群「タイプ」と同様の理由でこのHPでは単にブラベー格子と表現します。https://dictionary.iucr.org/Bravais_lattice ↩︎
- 空間群の剰余群と考えてもかまいませんし、極大部分群と考えても構いません。 ↩︎
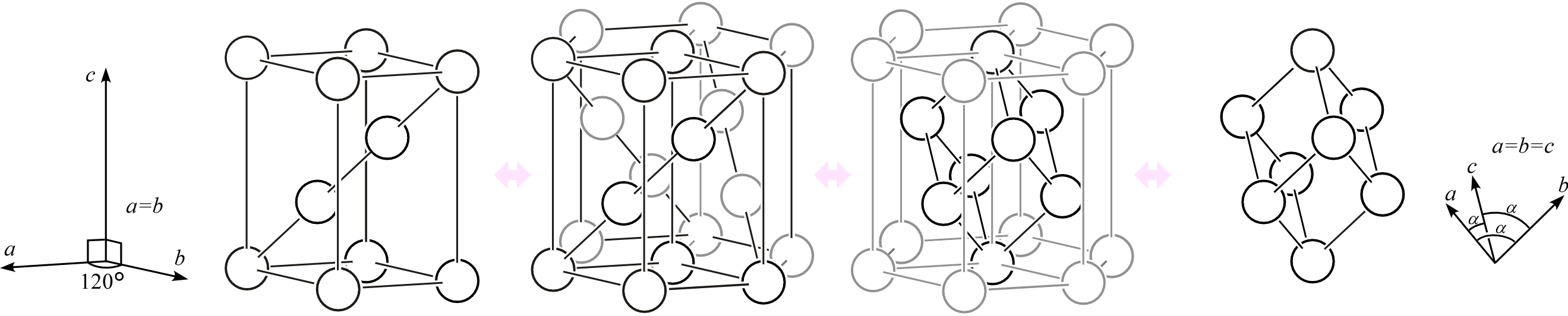
- 菱面格子の単位格子形状については、下図の左のような底面が菱形(すべての辺の長さが等しく内角が60°と120°)の直角柱ではなく、下図の右のような三辺の長さが等しくそれらが等しい角度 (\(\alpha\)) で交差する菱面体を考えてください。
 ↩︎
↩︎ - あえて六方格子の単位胞、すなわち底面が菱形(すべての辺の長さが等しく内角が60°と120°)の直角柱の対称性を表現すれば、その点群は \(mmm\)です。 ↩︎
- 点群は並進要素を含まないのに、並進要素を前提とした格子系と同じような分類をしようという発想に、そもそも若干の無理があるのです。このため後述する六方晶族のいびつさが生まれています。分子などの有限の大きさの物体形状を記述する際に結晶系はある程度の意味を持ちますが、並進要素を必ず含む結晶を取り扱う際にはむしろ格子系の概念の方が重要です。個人的な意見ですが、結晶を研究する人は結晶系よりも格子系に集中して学習した方が幸せになれるかもしれません。 ↩︎
- 三方晶系と六方晶系の違いは、回転あるいは回反の次数が「3」か「6」かの違いじゃないの?と考える方がいるかもしれませんが、そこまで単純な話ではないのです。六方晶系の点群 \(\bar{6}\)は、\(3/m\)という表現と等価ですから次数だけでは判断できません。さらに、回反ではなく回映という対称要素で考える (\(\bar{3} = S_6\), \(\bar{6} = S_3\)) と、見かけ上の次数が変わるのです。 ↩︎