Seto's Page

結晶系と\(a, b, c\)軸

　3次元の空間群は、群論的には230種類に分類されます。どの空間群も無数の並進操作を含んでおり、人間はその中の独立な3つを選んで \(a, b, c\) 軸と名付けます。もちろん、どれをどんな順番で選んでも空間群の性質(=結晶の性質)が変わるわけではありません。だったら好き勝手に選んでもいいような気がしますが、個人差が出ないようにある程度方針を決めておくほうが良い、と昔の結晶学者は考えました。このページでは標準表記の空間群ではどのような方針で \(a, b, c\) 軸が選ばれているのかをざっくり説明します。

　第一の方針は、右手系で \(a, b, c\) 軸を選ぶということです。これを統一しておかないと、例えばらせん軸 \(3_1\) の回転方向が人によって異なるという混乱が生じてしまいます。

　第二の方針は、なるべく短い並進ベクトルを3つ選び、それらが作る平行六面体の体積を最小にする、というものです。このような格子は基本単位格子と呼ばれます。ただし、基本単位格子の形状がその空間群の属する点群の対称性を満たさない場合、この原則は無視します(詳しい説明は「格子定数・結晶系・ブラー格子」ページを参照)。立方晶系の場合、この方針に従うだけで立方体形状の単位格子が一意に定まります(\(a, b, c\) は等価なのでどの順番で選んでもよい)。しかしそれ以外の結晶系の場合、この方針だけでは単位格子は一意に定まりません。

　第三の方針は、回転・回反・らせん軸に平行な方向や、鏡映・映進の法線方向を、\(a, b, c\) 軸のどれかに対応させるというものです。三斜晶系を除く各晶系では、結晶の方向をユニークに特徴づける次数が2以上の回転・回反・らせん・鏡映・映進を持ちます。これを主軸あるいは副軸とよびます。HM表記では主軸、副軸1、副軸2の順番に対称要素の記号を並べます。すでに1.3. で紹介済みですが各晶系における主軸・副軸のセッティングを再掲します。

結晶系	Primary 主軸	Secondary 副軸1	Tertiary 副軸2
三斜晶系 (triclinic)	–	–	–
単斜晶系 (monoclinic)	\(b\)	–	–
直方晶系 (orthorhombic)	\(a\)	\(b\)	\(c\)
正方晶系 (tetragonal)	\(c\)	\(a=b\)	\([110]\) = \([1\bar{1}0]\)
三方晶系 (Trigonal) 六方晶系 (hexagonal)	\(c\)	\(a\) = \(b\) = \([\bar{1}\bar{1}0]\)	\([1\bar{1}0]\) = \([120]\) = \([\bar{2}\bar{1}0]\)
立方晶系 (cubic)	\(a\) = \(b\) = \(c\)	\([111]\) = \([\bar{1}11]\) = \([1\bar{1}1]\) = \([11\bar{1}]\)	\([110]\) = \([1\bar{1}0]\) = \([011]\) = \([01\bar{1}]\) = \([ 101]\) = \([\bar{1}01]\)

もう少し言葉で補足しておきます。

• 三斜晶系: ユニークな方向が存在しないので、方針なし。ただし、なるべく\(\alpha,\beta,\gamma\)が90°に近くなるように \(a, b, c\) を選ぶことが多い。
• 単斜晶系: 次数が2の回転・回反・らせん・鏡映・映進のいずれかをもつ。その方向で最短の並進ベクトルを \(b\) 軸とする。\(b\) 軸に垂直で短い並進ベクトルを2つ選び、\(a, c\) 軸とする。ただしその選び方に任意性が残る。
• 直方晶系: 次数が2の回転・回反・らせん・鏡映・映進のいずれかを三つもち、それらは直交している。それら三方向で最短の並進ベクトルを\(a, b, c\) 軸とする。ただし、選ぶ順番には任意性が残る。
• 正方晶系: 次数が4の回転・回反・らせんを一つもつ。その方向で最短の並進ベクトルを \(c\) 軸とする。さらにc軸に垂直で、最短の並進ベクトルを \(a\) あるいは \(b\) 軸とする。\(a\) と \(b\) は等価なのでどの順番で選んでもよい。
• 三方晶系, 六方晶系 (六方格子): 次数が 3 あるいは 6 の回転・回反・らせんのいずれかをもつ。その方向で最短の並進ベクトルを\(c\)軸とする。さらに \(c\) 軸に垂直で、最も短い並進ベクトルを \(a\) 軸あるいは \(b\) 軸とする。\(a\) と \(b\) は等価なのでどの順番で選んでもよい。
• 三方晶系 (菱面格子): 次数が3の回転・回反のいずれかをもつ。それと斜交する最短の並進ベクトルを \(a, b, c\) 軸とする。\(a, b, c\) は等価なのでどの順番で選んでもよい。

　もうお分かりかと思いますが、第三の方針を守ったとしても、三斜、単斜、直方、三方晶系については \(a, b, c\) 軸を一意に決めることはできません。

　三斜晶系の場合は、ユニークな方向がありませんから万人共通の \(a, b, c\) 軸の選び方を決めようがありません。ただし、選び方によって空間群表記が変わることはないので、混乱もありません。

　三方晶系の場合、六方格子 (hexagonal setting)と菱面格子(rhombohedral setting) の両方をとることができます。どちらを優先するという決まりはなく、International Tablesには両方の場合が併記されています。詳しくは「三方/六方晶系の話題」ページをご覧ください。

　さて、多くの研究者の頭を悩ませるのは、単斜晶系と直方晶系に属する空間群に見られる「軸の選び方問題」です。以下に詳述します。

---

直方晶系の場合

　直方晶系は、次数が 2 の対称操作(回転・回反・らせん・鏡映・映進)を3つ含み、それらは互いに直交します。3つの方向は単位格子の3辺を構成しますが、それらを \( a, b, c\) とどのように対応付けるかは自明ではありません。例えば軸の長さが大きい順に \( a, b, c\) を対応させたい人もいるでしょうし、結晶構造(原子位置)と関連付けたい人もいるでしょう。もちろん好き勝手に選んでいいのですが、そうすると標準の空間群表記に一致しなくなるかもしれません。ここでは直方晶系における軸設定を説明します。

　直方晶系に属する \(Pma2\) という空間群があります。この空間群は \(a\) 軸に垂直な\(m\) 鏡映、\(b\) 軸に垂直な \(a\) 映進、\(c\) 軸に平行な2回回転を有しています。\(Pma2\) という表記をだれもが採用するのであれば、それぞれの軸はユニークな対称操作と結びついているので \(a, b, c\) の選び方に混乱は生まれません。ただ、なんらかの事情で軸設定を変更したい、という人がいたらどうしましょう。要望に応えるためには、軸設定だけでなく空間群の表記も変えなければいけません。直交する3つの方向に対して、右手系を維持したまま \( a, b, c\) 軸を割り当てることを考えると、以下のような6つのケースに分類できることが分かります。

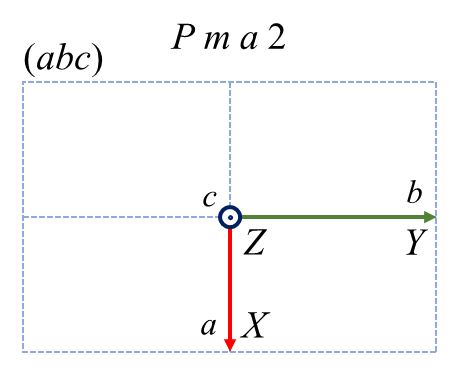
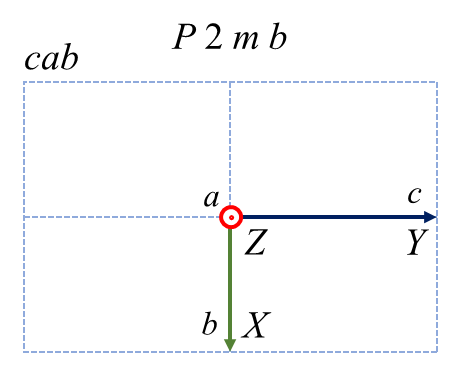
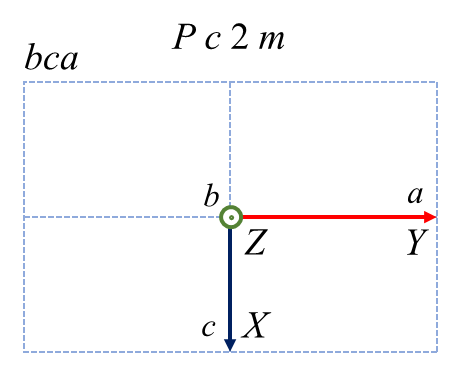
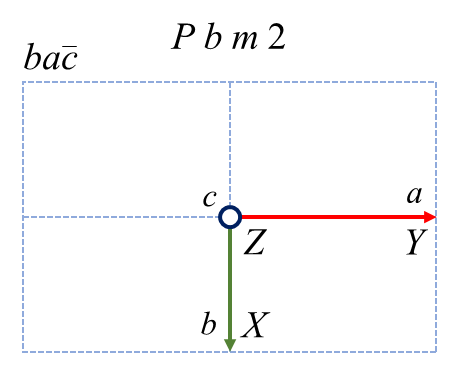
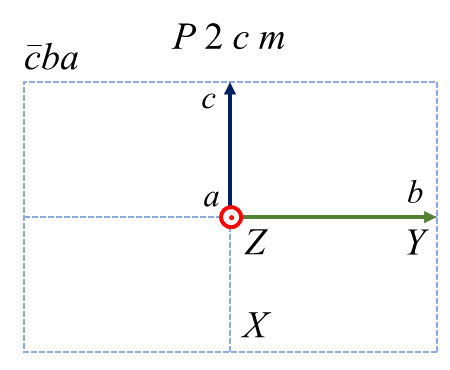
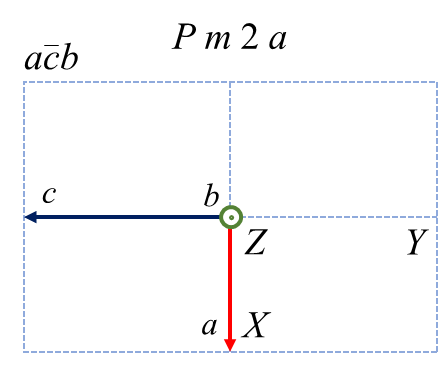
　赤、緑、青が\( a, b, c\) 軸に対応します。左上が標準の軸設定で、それ以外は非標準です。各図の左上に書かれた \(ba\bar{c}\) などの記号は軸設定をあらわす補助記号¹です。上段は \( a, b, c\) を巡回させたケースであり、各軸の正の向きは保存されます。下段は1つの軸を保存して残り2つを入れ替えたケースであり、その結果1つの軸の向きが反転しています。6つのケースは空間群表記こそ異なれ、全く同じ空間群の性質を示しています。どれが優れているわけでもないのですが、この中の1つ \(Pma2\) を標準にすることを昔の偉い人が決めました。なお、直方晶系だからといって必ずこの例のように表記が変化するとは限りません。例えば空間群 \(P222\)や \(Pmmm\) などは 3方向とも同じ記号なので \( a, b, c\) の順番を変えても表記は変化しません。

　さて、特段の事情がない限りは、標準の空間群表記と軸設定を使うべきです。ただし、歴史的な事情 (例えば古い文献で非標準の表記採用されている場合) や、相転移前後の格子定数の関係を考慮したい場合などは、非標準の空間群を使った方が良いかもしれません。その場合は空間群だけでなく以下のように原子位置も変換しなければいけませんので注意しましょう。

	\(cab\)	\(bca\)	\(ba\bar{c}\)	\(\bar{c}ba\)	\(a\bar{c}b\)
\(abc\) から変換	$$z, x, y$$	$$y, z, x$$	$$y,x,\bar{z}$$	$$z,y,\bar{x}$$	$$x,z,\bar{y}$$
\(abc\) へ変換	$$y, z, x$$	$$z, x, y$$	$$y,x,\bar{z}$$	$$\bar{z},y,x$$	$$x,\bar{z},y$$

　

---

単斜晶系の場合

　単斜晶系の空間群は次数が2の対称操作 (回転・回反・らせん・鏡映・映進のいずれか)を必ず含みます。このユニークな方向を\(b\) 軸と一致させるのが、IUCr (国際結晶学会)標準であり、この設定を2nd settingといいます。1st settingや3rd settingはそれぞれ\(a, c\) 軸がユニークな方向として定義されますが、標準ではありません。なぜ\(a\) 軸や\(c\) 軸を標準にしないのか？中途半端じゃない？、と思う人が大半だと思いますが、遠い昔に決まってしまったことなので、受け入れるしかありません。

　単斜晶系の中には\(Cc\) という空間群があります。この空間群は対称操作として\(C\) 複合格子と主軸(\(b\) 軸)に垂直な\(c\) 映進面を持っています。複合格子の並進ベクトルは\(\frac{a+b}{2}\) であり、\(c\) 映進面の並進ベクトルは\(\frac{c}{2}\) ですから、この表記によって残りの\(a, c\) 軸は自動的に決まるわけです。さてこの空間群について、あるひねくれものが「主軸は\(b\) 軸のままでいいけど\(a, c\) 軸は好きに選ばせてくれ」と考えたとします。そうすると、以下の6つケースがあることに気づくでしょう。(注: 主軸を明確にするために、\(Cc\) ではなく\(C1c1\) のように空間群を表記しています)

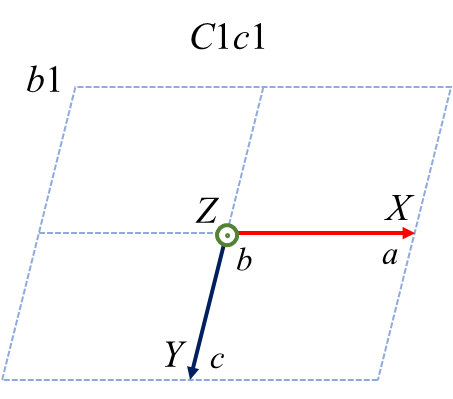
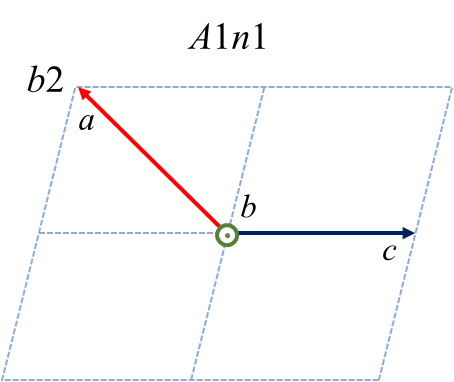
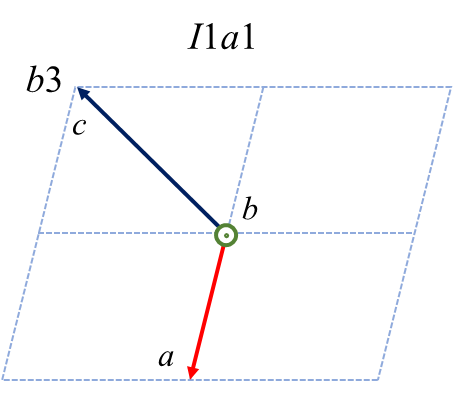
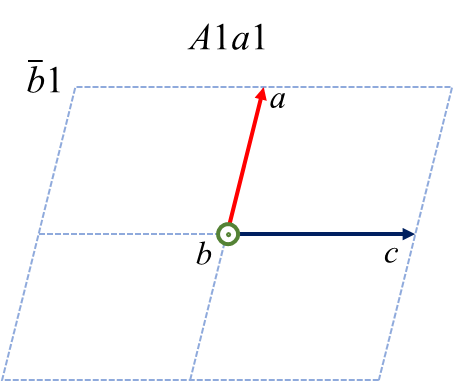
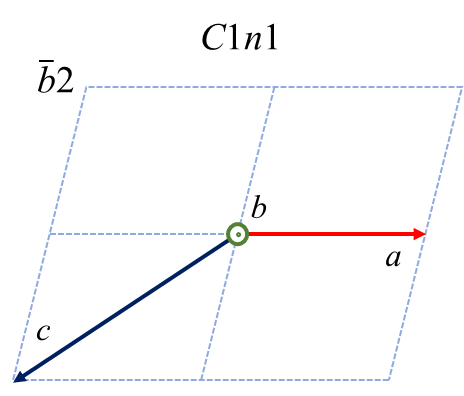
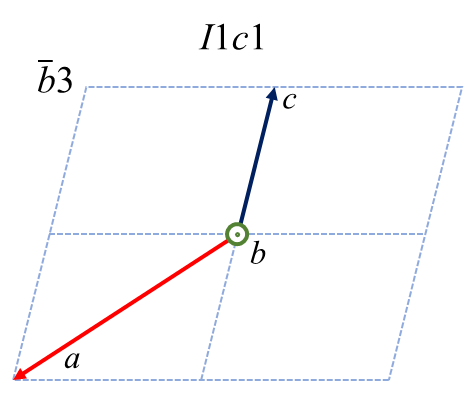
　赤、緑、青が\( a, b, c\) 軸に対応します。紙面垂直手前方向が主軸です。複合格子や映進面の記号が変化するので面食らいますが、これら6つのケースは全て2nd settingですし、単位格子の体積も同じです。優劣関係はありません。そうするとなぜ\(C1c1\) が標準表記として採用されたのか不思議ですが、私は経緯を良く知りません。どれか一つを選ぶ数学的理由はありませんので、きっと昔の人がエイやと好みで決めたんでしょう。

　上図中の記号 \(b1, b2\) などは軸設定を表す補助記号²です。標準設定で表記された結晶中の原子位置を非標準の設定に変換する、あるいはその逆変換をするための情報を以下にまとめました。

	\(b2\)	\(b3\)	\(\bar{b}1\)	\(\bar{b}2\)	\(\bar{b}3\)
\(b1\) から変換	$$\bar{z}, y, x+\bar{z}$$	$$z+\bar{x}, y, \bar{x}$$	$$\bar{z}, y, x$$	$$x+z, y, z$$	$$\bar{x}, y, \bar{x}+\bar{z}$$
\(b1\) へ変換	$$z+\bar{x}, y, \bar{x}$$	$$\bar{z}, y, x+\bar{z}$$	$$z, y, \bar{x}$$	$$x+\bar{z}, y, z$$	$$\bar{x}, y, x+\bar{z}$$

　さて、主軸を\(b\) 軸ではなく\(a\) や\(c\) 軸にしたいという、さらにひねくれた人がいらっしゃるかもしれません。まず\(a\) を主軸とした時の6つのケースおよび変換の仕方を示します。

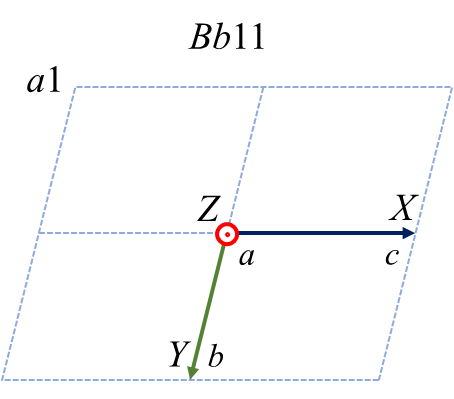
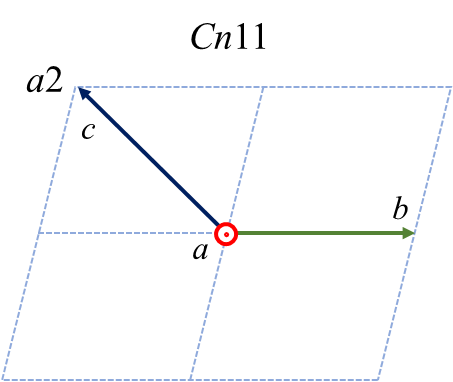
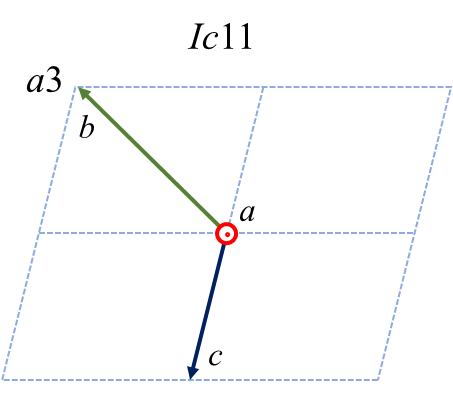
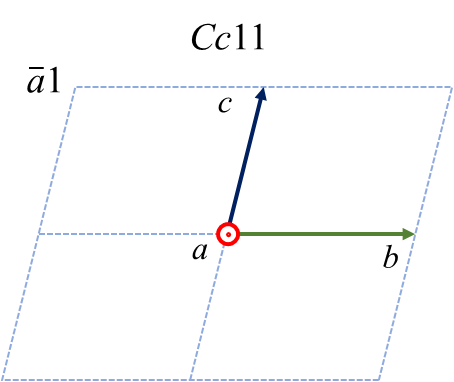
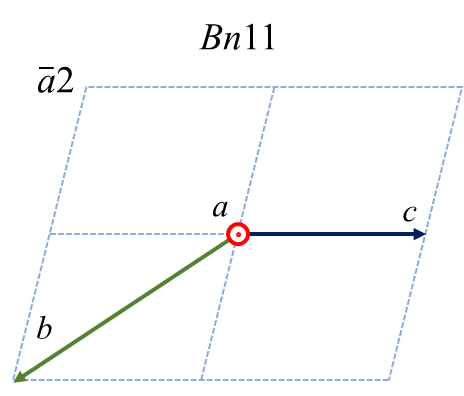
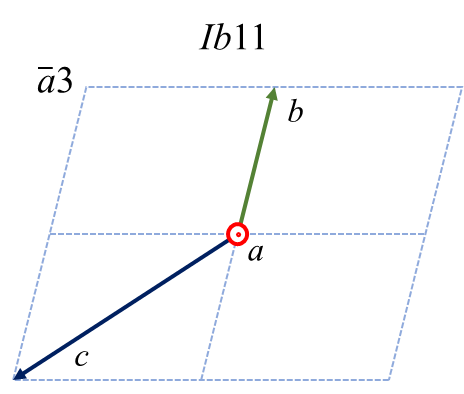
	\(a1\)	\(a2\)	\(a3\)	\(\bar{a}1\)	\(\bar{a}2\)	\(\bar{a}3\)
\(b1\) から変換	$$y, z, x$$	$$y, x+\bar{z}, \bar{z}$$	$$y, \bar{x}, z+\bar{x}$$	$$y, x, \bar{z}$$	$$y, z, x+z$$	$$y, \bar{x}+\bar{z}, \bar{x}$$
\(b1\) へ変換	$$z, x, y$$	$$y+\bar{z}, x, \bar{z}$$	$$\bar{y}, x, z+\bar{y}$$	$$y, x, \bar{z}$$	$$z+\bar{y}, x, y$$	$$\bar{z}, x, z+\bar{y}$$

　最後に、\(c\) を主軸とした時の6つのケースおよび変換の仕方を示します。

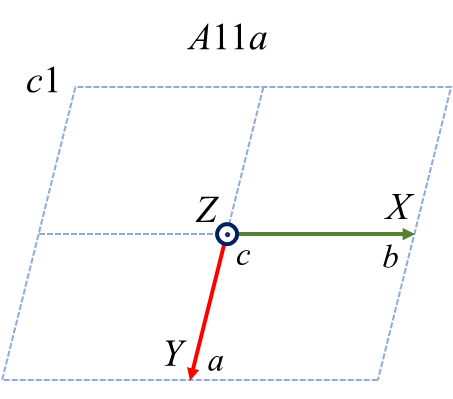
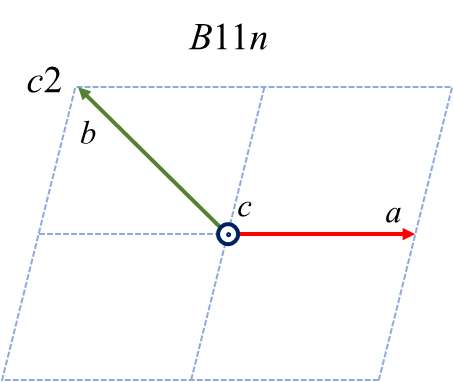
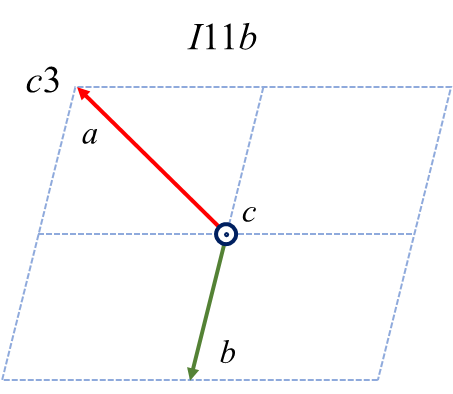
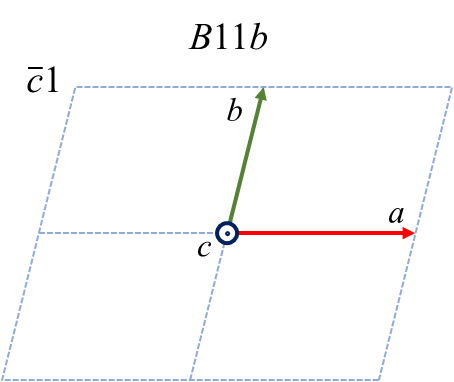
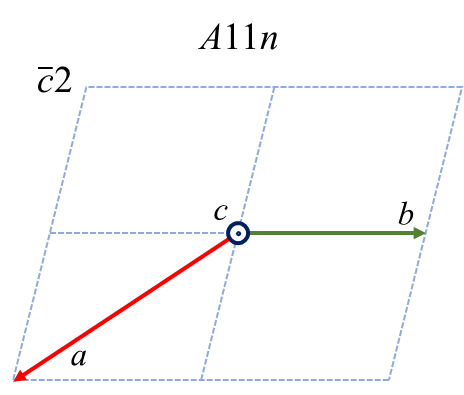
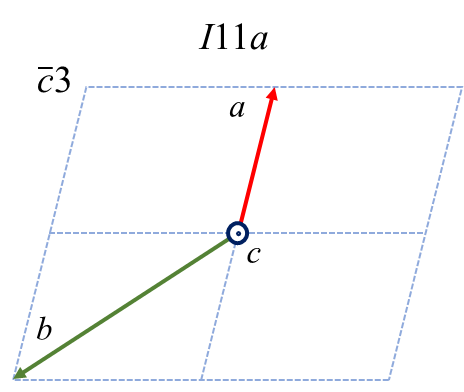
	\(c1\)	\(c2\)	\(c3\)	\(\bar{c}1\)	\(\bar{c}2\)	\(\bar{c}3\)
\(b1\) から変換	$$z, x, y$$	$$x+\bar{z}, \bar{z}, y$$	$$\bar{x}, z+\bar{x}, y$$	$$x, \bar{z}, y$$	$$z, x+z, y$$	$$\bar{x}+\bar{z}, \bar{x}, y$$
\(b1\) へ変換	$$y, z, x$$	$$x+\bar{y}, z, \bar{y}$$	$$\bar{x}, z, y+\bar{x}$$	$$x, z, -y$$	$$y+\bar{x}, z, x$$	$$\bar{y}, z, y+\bar{x}$$

---

1. 「空間群一覧」ページでは、「Axis setting, Origin」 という列に記載しています。 ↩︎
2. 同上 ↩︎