2.1. 群、点群、空間群とは

群とは

　空(くう)ではない集合 $G$ があり、そこに含まれる要素のことを元 (element) と呼ぶことにします。元と元との間に何らかの算法 (operation, $\otimes$と表現します)が定義され、その算法の結果も必ず集合 $G$ に含まれるとします。このような集合 $G$ が、次の三つの条件を満たすとき、その集合を群 (group) とよびます。

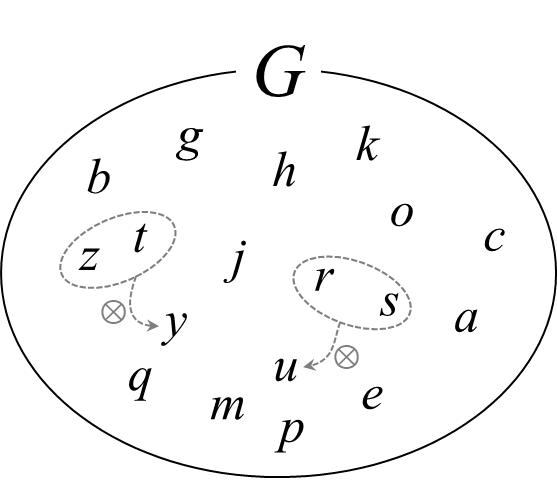
結合則の成立: 任意の元 $g, h, k$ について、$ g \otimes (h\otimes k)=(g\otimes h)\otimes k $ を満たす。
単位元の存在: 任意の元 $g$ に対して、 $g \otimes e = e \otimes g =g $ となるような元 $e$ が存在する ($e$ を単位元と呼ぶ)。
逆元の存在: 任意の元 $g$ に対して、 $g \otimes x = x \otimes g = e$ となるような元 $x$が存在する ($x$ を$g$ の逆元と呼び、$g^-1$ と表現する)。

単位元 $e$ しか含まれない集合も群ですし、元が無限個あるような群もあります。ある元とその逆元が同一になることもあります。さらに次の条件を満たすとき、アーベル群あるいは可換群といいます。

交換則: 任意の元 $g, h$ について、$ g \otimes h =h \otimes g $ を満たす。

抽象的な定義で分かりにくいですね。具体例を挙げながら群の性質を見ていきます。

行列を元とする群

　行列は、積や和などが定義可能な線形代数表現です。行列の積や和は条件1 (結合則)を満たすので、うまく行列を集めれば群を作ることができます。なお以降は、行列は全て正方行列であり、群の算法はかけ算であるとします。また、いちいち算法($\otimes$)の記号を書くのも冗長ですので省略します。行列を並べて書いたらそれはかけ算だと思ってください。

　行列を元とする群があったとすると、そこには必ず単位行列が含まれるはずです (条件2 単位元の存在)。また、どんな元にも必ず逆元を持たないといけません(条件3 逆元の存在)から、正則行列 (= 逆行列をもつ = 行列式(determinat)がゼロではない)である必要もあります。もちろん、群から任意の元を二つ取り出して掛算した結果は、群のいずれかの元に一致しなければいけないという大前提もあります。行列の演算は可換ではありません (かけ算の順序を変えると結果が異なることがある)ので、条件4 (交換則)を満たすとは限りません。

具体例

　以上を踏まえて具体例を見てみましょう。例えば、4行4列の単位行列($e$)を一つだけ含む集合は、群となります。単位行列の逆元はそれ自身です。
$$ \begin{pmatrix}1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix}
$$ 単位行列($e$)と、その符号を全てマイナスにした行列($-e$)の、二つを含む集合も、群となります。それぞれが、自分自身の逆元となります。
$$
\begin{pmatrix}1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}-1&0&0&0 \\ 0&-1&0&0 \\ 0&0&-1&0 \\ 0&0&0&-1 \end{pmatrix}
$$以下のような4つの行列も群となります。最後の二つは互いに逆元の関係になっています。$$
\begin{pmatrix}1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}-1&0&0&0 \\ 0&-1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}0&1&0&0 \\ -1&0&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}0&-1&0&0 \\ 1&0&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix}
$$元の数は無限にあっても構いません。例えば4列目の1~3行目が$r($任意の実数)の倍数であるような以下の集合も群となります。$$
\cdots,
\begin{pmatrix}1&0&0&-r \\ 0&1&0&-r \\ 0&0&1&-r \\ 0&0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}1&0&0&r \\ 0&1&0&r \\ 0&0&1&r \\ 0&0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}1&0&0&2r \\ 0&1&0&2r \\ 0&0&1&2r \\ 0&0&0&1 \end{pmatrix} ,\ \
\cdots,$$

　群に含まれる元の数を、位数といいます。直上の例では、位数は無限ということになります。

生成元

　生成元 (generator)とは、その名の通り群を生成する元のことです。ある群 $G$ の中からなるべく少ない個数の元 $s_1, s_2, \cdots$ を選び、それら及びそれらの逆元 $s_1^{-1}, s_2^{-1}, \cdots$ を何回でも好きなだけかけ合わせて (同じものを使っても構わない)、もし群 $G$ の元をすべて網羅することができたら、 $s1, s2, \cdots$ を群 $G$ の生成元であるといいます。

　例えば、先ほども挙げた以下の場合 (分かりやすくするため $s_1, s_2, \cdots$ と記号を振ります)、$$
s_1=\begin{pmatrix}1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} ,\ \
s_2=\begin{pmatrix}-1&0&0&0 \\ 0&-1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} ,\ \
s_3=\begin{pmatrix}0&1&0&0 \\ -1&0&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} ,\ \
s_4=\begin{pmatrix}0&-1&0&0 \\ 1&0&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix}
$$ $s_3$を選び、それを何回もかけ合わせると、 $s_3^2 = s_2,\ s_3^3 = s_4,\ s_3^4= s_1$ という関係が見出されますので、 $s_3$ はこの群の生成元であるといえます。同様に $s_4$ もこの群の生成元です。一方、$s_2$ は $s_2^2 =s_1, s_2^3 =s_2$ のように $s_1$ しか生み出せませんから、この群の生成元とは言えません。また、$s_1$ (単位元) も $s_1$ しか生み出せないのでやはりこの群の生成元とは言えません。

　上の例では $s_3$ あるいは $s_4$ が生成元でした。どちらか一つを選べばよく、両方を選ぶ必要はありません。このように、ある群の生成元が1つだけで表現できるとき、その群は巡回群 (cyclic group) である、といいます。「巡回」という言葉からは、上の例のような元の数 (位数) が有限の場合に限定されるような気がします。しかし位数が無限の群だとしても、生成元が1つだけであれば、巡回群です。無限(infinite)巡回群ということもあります。たとえば「具体例」の最後に示した群の場合は、$$
\begin{pmatrix}1&0&0&-r \\ 0&1&0&-r \\ 0&0&1&-r \\ 0&0&0&1 \end{pmatrix} \ \ or \ \ \begin{pmatrix}1&0&0&r \\ 0&1&0&r \\ 0&0&1&r \\ 0&0&0&1 \end{pmatrix}$$が生成元となります。

行列と対称操作

　別ページで説明している通り、すべての対称操作は4×4正則行列のユークリッド変換で表現することが出来ます。点群や空間群とは、対称操作を元とする群のことです。「操作が元である」とはイメージしにくい表現ですね。操作が作用するのは、何らかの物体の座標です。ある操作によって物体の座標を別の座標に写すということは、線形代数的には物体の座標に同じ次元の正方行列をかけることと等価です。つまり、座標に作用する「操作」とは、座標にかけあわせる「行列」とみなすことができます。以降では、行列とは単に数値を縦横に並べたものではなく、対称操作の性質をもつのだと思って読み進めて下さい。

点群

　点群は、並進(平行移動)を含まず、原点を不動にするような対称操作を組み合わせてできる群です。並進を含まない対称操作には回転、回反、対称心、鏡映がありますが、それらが原点を不動にするような操作である時、アフィン変換行列の4列目は必ず 0,0,0,1 になります¹。
並進を含まない対称操作: $ \begin{pmatrix}
A_{11} & A_{12} & A_{13} & 0\\
A_{21} & A_{22} & A_{23} & 0\\
A_{31} & A_{32} & A_{33} & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
= \begin{pmatrix}
\huge{A} & \begin{matrix}0\\0\\0\end{matrix} \\
\begin{matrix}0&0&0\end{matrix} & 1
\end{pmatrix}$

　4行目と4列目が 0,0,0,1 の行列をどのように掛け合わせても、4行目と4列目は 0,0,0,1 になりますので、簡単のために以降は $A$ の部分だけで対称操作を表現することにします。

具体例

　例えば$Z$軸と一致する$2$回回転軸をもつ対称性は、以下のような2つの行列からなる群であると言えます。1つ目が恒等変換(単位行列)、2つ目が180度回転操作を表します。これは点群$2$に対応します。$$ \begin{pmatrix}1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}-1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix}
$$もし、この点群$2$に、以下のように90°回転操作(3つ目)も加えたらどうなるでしょう。ちょっと考えたら分かりますが、2つ目と3つ目の掛け算の結果として4つ目の270°回転操作も加えないと、群として成立しません。4つ揃って点群 $4$ となります。$$
\begin{pmatrix}1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}-1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}0&1&0 \\ -1&0&0 \\ 0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}0&-1&0 \\ 1&0&0 \\ 0&0&1 \end{pmatrix}
$$今度は、点群 $2$ に$Z$軸に垂直な鏡映操作(3つ目)を加えてみましょう。先ほどと同じような理屈で4つ目の対称心操作($\bar{1}$)が必然的に生み出されてしまいます。これが点群 $2/m$ です。
$$
\begin{pmatrix}1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}-1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}1&0&0 \\ 0&1&0 \\ 0&0&-1 \end{pmatrix} ,\ \
\begin{pmatrix}-1&0&0 \\ 0&-1&0 \\ 0&0&-1 \end{pmatrix}
$$最後の例として、$Y$ 軸に一致する180°回転操作(3つ目)も加えてみましょう。やはり4つ目の対称操作($X$ 軸に一致する180°回転操作)が生み出されてしまいます。これら4つで点群 $222$ となります。
$$
\begin{pmatrix}1&0&0 \\ 0&1&0 \\ 0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}-1&0&0 \\ 0&-1&0 \\ 0&0&1 \end{pmatrix} ,\ \
\begin{pmatrix}-1&0&0 \\ 0&1&0 \\ 0&0&-1 \end{pmatrix} ,\ \
\begin{pmatrix}1&0&0 \\ 0&-1&0 \\ 0&0&-1 \end{pmatrix}
$$

　このように、もとの点群に別の対称要素を加えていくことで、次々と別の点群を生成することが出来ます。

空間群

　空間群の群としての構造を行列で表現する場合、アフィン変換の表現、すなわち4×4行列を使う必要があります。並進を考慮しなければいけないからです。またこの行列が変換するのは、mとかÅのような長さの次元をもつ座標ではなく、単位格子ベクトル $a, b, c$ をそれぞれ何倍するかを示す分率座標 $(u \ v \ w \ 1)$ であることにご注意ください。最後の1はダミー次元です。実際の空間での座標は $ua+vb+wc$ となります。ベクトル $a, b, c$ は長さが違うかもしれませんし、直交するとも限りません。

　以降の説明では、 $u, v, w$ を $X, Y, Z$ 軸に対応させた分率座標空間を考えます。例えば $X$ 軸方向に $x$ 進むということは、 $a$ ベクトルを $x$ 倍した量だけ進むという意味になります。

並進群

　結晶は単位格子並進で空間を埋め尽くすような物質です。3次元の単位格子並進操作は、

$$\cdots,
\begin{pmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&1&-1 \\ 0&0&0&1\end{pmatrix} ,
\begin{pmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&1&0 \\ 0&0&0&1\end{pmatrix} ,
\begin{pmatrix}1&0&0&1\\ 0&1&0&0\\ 0&0&1&0 \\ 0&0&0&1\end{pmatrix} ,
\begin{pmatrix}1&0&0&0\\ 0&1&0&1\\ 0&0&1&0 \\ 0&0&0&1\end{pmatrix} ,
\begin{pmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&1&1 \\ 0&0&0&1\end{pmatrix} ,\\
\begin{pmatrix}1&0&0&1\\ 0&1&0&1\\ 0&0&1&0 \\ 0&0&0&1\end{pmatrix} ,
\begin{pmatrix}1&0&0&1\\ 0&1&0&0\\ 0&0&1&1 \\ 0&0&0&1\end{pmatrix} ,
\begin{pmatrix}1&0&0&0\\ 0&1&0&1\\ 0&0&1&1 \\ 0&0&0&1\end{pmatrix} ,
\begin{pmatrix}1&0&0&1\\ 0&1&0&1\\ 0&0&1&1 \\ 0&0&0&1\end{pmatrix} ,
\begin{pmatrix}1&0&0&2\\ 0&1&0&1\\ 0&0&1&1 \\ 0&0&0&1\end{pmatrix} , \cdots $$

のような、左上3行3列が単位行列で4列1~3行にあらゆる整数を含む、無限個の（アフィン変換）行列の集合で表現することができます。すべてを書き下すことはできないので、以下のような書き方でこの無限個の集合を表現することにします。

$ \begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3 \\ 0&0&0&1\end{pmatrix}$ ただし、$n_1, n_2,n_3$はすべての整数

この集合が群の構造を持つことは、ここまで読んだ方なら容易に理解できるでしょう。単位元は $n_1 = n_2 = n_3=0$ とすればよいですし、逆元は $n_1, n_2,n_3$ の符号を反転するだけです。このような群を、並進群といいます。何の面白みもない群ですが、空間群は必ず並進群を部分群として含みますので、超重要です。なお、上で示した並進群は単純格子に対応しており、このタイプの並進群だけを含む空間群が $P1$ です。並進群には、この他に底心格子、体心格子、面心格子に対応するものがあります。以下に列記します。以降は $n_1, n_2, n_3$ がすべての整数を表すとします。

底心(C)の並進群
$$ \begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3 \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&n_1+\frac{1}{2}\\ 0&1&0&n_2+\frac{1}{2}\\ 0&0&1&n_3\\ 0&0&0&1\end{pmatrix} $$

体心格子の並進群
$$ \begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3 \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&n_1+\frac{1}{2}\\ 0&1&0&n_2+\frac{1}{2}\\ 0&0&1&n_3+\frac{1}{2}\\ 0&0&0&1\end{pmatrix} $$

面心格子の並進群
$$ \begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3 \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2+\frac{1}{2}\\ 0&0&1&n_3+\frac{1}{2}\\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&n_1+\frac{1}{2}\\ 0&1&0&n_2\\ 0&0&1&n_3+\frac{1}{2}\\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&n_1+\frac{1}{2}\\ 0&1&0&n_2+\frac{1}{2}\\ 0&0&1&n_3\\ 0&0&0&1\end{pmatrix} $$

くどいようですが、 $n_1, n_2, n_3$ はすべての整数を表しています。並進群の元の数は無限個であることを忘れないようにしてください。

並進群+対称操作

　点群の時と同様に、並進群に別の対称要素を加えることで新しい空間群を生み出していきましょう。

　まず、空間群$P1$に対称心操作を加えてみましょう。群として成立するためには、以下のような行列集合のすべてを元として含まないといけません。1つ目の行列集合が並進操作で、2つ目の集合が対称心操作に対応します。対称心操作をひとつ加えたつもりでも、並進操作によって増殖し、無限個の集合となることに注意しましょう。これが空間群$P\bar{1}$ の行列表現です。
$$ \begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3 \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}-1&0&0&n_1\\ 0&-1&0&n_2\\ 0&0&-1&n_3 \\ 0&0&0&1\end{pmatrix}
$$

　今度は $P1$ に $Y$ を軸とする $2_1$ らせん操作を加えてみます。これは空間群 $P2_1$ に対応します。
$$ \begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3 \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}-1&0&0&n_1\\ 0&1&0&n_2+\frac{1}{2}\\ 0&0&-1&n_3 \\ 0&0&0&1\end{pmatrix}$$

　$X, Y, Z$ 軸がすべて $2_1$ らせん操作であると考えてみます。2, 3, 4つめの行列はそれぞれ $X, Y, Z$ 軸と一致する $2_1$ らせん操作に対応します。これは空間群 $P2_12_12_1$ に対応します。
$$ \begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3 \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&n_1+\frac{1}{2}\\ 0&-1&0&n_2\\ 0&0&-1&n_3 \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}-1&0&0&n_1\\ 0&1&0&n_2+\frac{1}{2}\\ 0&0&-1&n_3 \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}-1&0&0&n_1\\ 0&-1&0&n_2\\ 0&0&1&n_3+\frac{1}{2} \\ 0&0&0&1\end{pmatrix}$$

　並進群を $C$ 底心格子として、$Y$ 軸に垂直な $c$ 映進面操作を考えてみましょう。2つめが $C$ 底心操作、3つめが $c$ 映進操作に対応し、4つめは2つめと3つめの積で現れる操作($Y=1/4$ 面に位置する $n$ 映進面)です。これが空間群 $Cc$ です

$$ \begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3 \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&n_1+\frac{1}{2}\\ 0&1&0&n_2+\frac{1}{2}\\ 0&0&1&n_3\\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&n_1\\ 0&-1&0&n_2\\ 0&0&1&n_3+\frac{1}{2} \\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&n_1+\frac{1}{2}\\ 0&-1&0&n_2+\frac{1}{2}\\ 0&0&1&n_3+\frac{1}{2}\\ 0&0&0&1\end{pmatrix} $$

　いくつかの例を見てもうお分かりだと思いますが、空間群の性質を理解するためには、単位格子ひとつ分の対称操作の関係をみるだけで十分です。また各行列の左上3行3列の部分だけを取り出せば、点群の構造とよく似ていることにも気づかれると思います。この類似性については別ページで解説します。

らせん操作や映進操作が作る群

　らせん操作や映進操作も並進をともなう対称操作です。ここでは並進群のことはいったん忘れて、たとえば $X$ 軸に一致する $2_1$ らせん操作$$S=\begin{pmatrix}1&0&0&\frac{1}{2}\\ 0&-1&0&0\\ 0&0&-1&0\\ 0&0&0&1\end{pmatrix}$$を生成元とするとどんな群を得られるか考えてみましょう。$j$を任意の整数として、$$ S^{2j}=\begin{pmatrix}1&0&0&j\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\end{pmatrix}$$という関係が容易に見出されますから、$S$を生成元とする群は以下のような2種類の行列集合のすべてをふくみます。

$ \begin{pmatrix}1&0&0&n\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}1&0&0&\frac{1}{2}+n\\ 0&-1&0&0\\ 0&0&-1&0\\ 0&0&0&1\end{pmatrix}
$ ただし$n$はすべての整数

一つ目の行列集合は $X$ 軸方向のみの並進群です。一方向のみとはいえ並進群を含みますから、この集合も立派な空間群ということになります。

　今度は、 $YZ$ 平面に一致して、並進量が $(0, \frac{1}{2}, \frac{1}{2})$ であるような $n$ 映進操作$$N=\begin{pmatrix}-1&0&0&0\\ 0&1&0&\frac{1}{2}\\ 0&0&1&\frac{1}{2}\\ 0&0&0&1\end{pmatrix}$$ を生成元としてみましょう。やはり$$ N^{2j}=\begin{pmatrix}1&0&0&0\\ 0&1&0&j\\ 0&0&1&j\\ 0&0&0&1\end{pmatrix}$$ という関係を考慮すれば、以下のような二つの行列集合を元とするような群であると考えることができます。

$ \begin{pmatrix}1&0&0&0\\ 0&1&0&n\\ 0&0&1&n\\ 0&0&0&1\end{pmatrix},
\begin{pmatrix}-1&0&0&0\\ 0&1&0&n\\ 0&0&1&n\\ 0&0&0&1\end{pmatrix}
$ ただし$n$はすべての整数

一つ目の行列集合は $Y+Z$ 軸方向の並進群です。これもやはり空間群です。

　最後に $XY, YZ, ZX$ 面のそれぞれに $n$ 映進操作 (それぞれ$N_1, N_2, N_3$とします)であるような状況を考え、これらを生成元として群を作ってみましょう。$$
N_1=\begin{pmatrix}1&0&0&\frac{1}{2}\\ 0&1&0&\frac{1}{2}\\ 0&0&-1&0\\ 0&0&0&1\end{pmatrix},\ \ N_2=\begin{pmatrix}-1&0&0&0\\ 0&1&0&\frac{1}{2}\\ 0&0&1&\frac{1}{2}\\ 0&0&0&1\end{pmatrix},\ \ N_3=\begin{pmatrix}1&0&0&\frac{1}{2}\\ 0&-1&0&0\\ 0&0&1&\frac{1}{2}\\ 0&0&0&1\end{pmatrix}
$$$j_1, j_2, j_3$を任意の整数とすれば、以下のような関係が容易に導かれます。$$
N_1^{2j_1}=\begin{pmatrix}1&0&0&j_1\\ 0&1&0&j_1\\ 0&0&1&0\\ 0&0&0&1\end{pmatrix},\ \ N_2^{2j_2}=\begin{pmatrix}1&0&0&0\\ 0&1&0&j_2\\ 0&0&1&j_2\\ 0&0&0&1\end{pmatrix},\ \ N_3^{2j_3}=\begin{pmatrix}1&0&0&j_3\\ 0&1&0&0\\ 0&0&1&j_3\\ 0&0&0&1\end{pmatrix}
$$$j_1, j_2, j_3$は任意の整数でしたから、$j_3+j_1, j_1+j_2, j_2+j_3$も任意の整数です。つまり、3次元の並進群が生み出されたわけです。また、$N_1, N_2, N_3$ から2つあるいは3つ選んでかけあわせると、$$
N_1 N_2 = \begin{pmatrix}-1&0&0&\frac{1}{2}\\ 0&1&0&1\\ 0&0&-1&-\frac{1}{2}\\ 0&0&0&1\end{pmatrix},\ \
N_2 N_3 = \begin{pmatrix}-1&0&0&-\frac{1}{2}\\ 0&-1&0&\frac{1}{2}\\ 0&0&1&1\\ 0&0&0&1\end{pmatrix},\\
N_3 N_1 = \begin{pmatrix}1&0&0&1\\ 0&-1&0&-\frac{1}{2}\\ 0&0&-1&-\frac{1}{2}\\ 0&0&0&1\end{pmatrix} ,\ \
N_1 N_2 N_3 = \begin{pmatrix}-1&0&0&0\\ 0&-1&0&0\\ 0&0&-1&-1\\ 0&0&0&1\end{pmatrix}
$$という関係が導かれます。既に並進群があることが分かっているので、4列目の1~3行については $1 \rightarrow 0$ 、$-\frac{1}{2} \rightarrow \frac{1}{2}$ と変換しても一般性を失いません。最初の3つは、それぞれ $N_1 N_2: Z=X=\frac{1}{2}$、$N_2 N_3: X=Y=\frac{1}{2}$、$N_3 N_1: Y=Z=\frac{1}{2}$ という直線と一致する2回回転操作に対応します。最後のひとつは原点に位置する対称心操作を意味します。結局、$N_1, N_2, N_3$ を生成元とする行列を書き下すと、以下のようになります。これは空間群 $Pnnn (=P 2/n\ 2/n\ 2/n)$ に対応する行列表現です。$$
\begin{pmatrix}1&0&0&n_1\\ 0&1&0&n_2\\ 0&0&1&n_3\\ 0&0&0&1\end{pmatrix}, \ \
\begin{pmatrix}1&0&0&\frac{1}{2}+n_1\\ 0&1&0&\frac{1}{2}+n_2\\ 0&0&-1&n_3\\ 0&0&0&1\end{pmatrix},\ \
\begin{pmatrix}-1&0&0&n_1\\ 0&1&0&\frac{1}{2}+n_2\\ 0&0&1&\frac{1}{2}+n_3\\ 0&0&0&1\end{pmatrix},\ \
\begin{pmatrix}1&0&0&\frac{1}{2}+n_1\\ 0&-1&0&n_2\\ 0&0&1&\frac{1}{2}+n_3\\ 0&0&0&1\end{pmatrix} \\
\begin{pmatrix}-1&0&0&\frac{1}{2}+n_1\\ 0&1&0&n_2\\ 0&0&-1&\frac{1}{2}+n_3\\ 0&0&0&1\end{pmatrix},\ \
\begin{pmatrix}-1&0&n_1&\frac{1}{2}+n_2\\ 0&-1&0&\frac{1}{2}+n_3\\ 0&0&1&1\\ 0&0&0&1\end{pmatrix},\ \
\begin{pmatrix}1&0&0&n_1\\ 0&-1&0&\frac{1}{2}+n_2\\ 0&0&-1&\frac{1}{2}+n_3\\ 0&0&0&1\end{pmatrix} ,\ \
\begin{pmatrix}-1&0&0&n_1\\ 0&-1&0&n_2\\ 0&0&-1&n_3\\ 0&0&0&1\end{pmatrix} $$

　以上の議論からわかるように、らせん軸操作や映進面操作を元に持つような群は、必然的に並進群を伴うことになります。言い換えると、らせん軸操作や映進面操作は、空間群(結晶)だけが持つ対称操作です。

脚注

並進を伴わないからといって、アフィン変換行列の4列目が 0, 0, 0, 1 になるとは限りません。例えば、$Z$軸に垂直で$Z=w$を通る鏡映は $$\begin{pmatrix}
1&0&0&0\\
0&1&0&0\\
0&0&-1&2w\\
0&0&0&1
\end{pmatrix}$$のように表現できますが、この行列は2回かけると単位行列に戻ります。 ↩︎