格子定数とベクトル
3次元の結晶の単位胞は、通常3方向の並進ベクトル \(\textbf{a}, \textbf{b}, \textbf{c}\) のそれぞれの長さ\(a,b,c\) と、それらの間の角度 \(\alpha,\beta,\gamma\) によって表現します。これら \(a,b,c,\alpha,\beta,\gamma\) の6つのパラメータを格子定数 (cell constants, lattice constants)といいます。特別な対称性の場合を除いて \(a,b,c\) の長さは等しいとは限りませんし \(\alpha,\beta,\gamma\) の角度が \(90^\circ\) とも限らないことに注意しましょう。
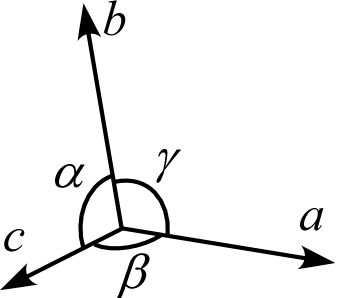
格子定数からベクトルへの変換
さて、6つの数値で表す格子定数はコンパクトな表現ではあるものの、様々な幾何学量を計算する際には単位格子ベクトルを直交座標系で成分表示する方が便利な場合も多いです。ただし、3つの単位格子ベクトル \(\mathbf{a}, \mathbf{b}, \mathbf{c}\) は直交するとは限りませんから、それぞれを直交座標系の \(X,Y,Z\) 軸に一致させることは一般的には不可能です。\(\mathbf{a}\) を \(X\) 軸に一致させたい人もいれば、\(\mathbf{c}\) を \(Z\) 軸に一致させたい人もいるでしょう。1つの軸の方向を決めたとて、まだ自由度は残ります。当然ながら万人が納得する唯一の正解はありません。ここでは、以下のような基準1で、格子定数 \(a,b,c,\alpha,\beta,\gamma\) を直交座標系で成分表示する方法を説明しましょう。
- \(\mathbf{c}\) を \(Z\) 軸に一致させる
- \(\mathbf{b}\) を \(YZ\) 平面上に一致させる
この基準に従えば、まず \(\mathbf{c}\) については \(\mathbf{c} = (0,0,c) \)と簡単に定義できます。次に \(\mathbf{b}\) については \(\mathbf{c}\) とのなす角が \(\alpha\) であることと \(YZ\) 平面に一致する (すなわち \(X=0\) である) ことを考慮して、\(\mathbf{b} = (0,b \sin\alpha,b \cos\alpha) \) とやはり簡単に定義できます。\(\mathbf{a}\) についてはちょっと複雑になりますが、既に求まっている \(\mathbf{b, c}\) との関係を考慮すれば、$$ \mathbf{a} = (a \sqrt{1-\cos^2\beta-\left(\frac{\cos\gamma-\cos\alpha \cos\beta}{\sin\alpha}\right)^2},\ \ a \frac{\cos\gamma-\cos\alpha \cos\beta}{\sin\alpha},\ \ a\cos\beta)$$となります2。以上のように \(\mathbf{a}, \mathbf{b}, \mathbf{c}\) を計算すれば、後は簡単なベクトル・行列の演算で逆単位格子ベクトルも求まりますし、さらにそれらを使って面間隔や面間の角度なども容易に計算できます3。
結晶中の方向と距離の表現
単位格子ベクトルは直行するとは限らず、長さが等しいとも限りません。このような座標系に対応する方向と距離を、結晶学の分野では角括弧 \([]\) (square brackets) を使って \([u\ v\ w]\) と表現します。\([u\ v\ w]\) は \(u\mathbf{a}+\mathbf{b}v+\mathbf{c}w\) と定義されるベクトルのことです。言い換えると、\([u\ v\ w]\) は \(\mathbf{a}, \mathbf{b}, \mathbf{c}\) を基底とするベクトル空間中の座標を意味しており、\(\mathbf{a}, \mathbf{b}, \mathbf{c}\) を基底ベクトルということもあります。
\(u,v,w\) にどんな実数を入れても構いませんが、整数のみで構成される場合は格子点と格子点を結ぶことになるので必ず「並進」ベクトルの性質を持ちます (例えば \([100]\) は \(\mathbf{a}\) そのもの、 \([211]\) は\(2\mathbf{a}+\mathbf{b}+\mathbf{c}\) )。また、負の数値を表現するときはマイナスではなく数字の上にバーをつける4ほうが好ましいです (例えば \([1\bar{1}1]\))。
結晶の対称性によっては、複数の方向が等価な関係になることがあります。例えば \([100]\) と \([010]\) が結晶学的に等価である場合、山括弧 \(\langle\rangle\) (angle brackets) を使って \(\langle100\rangle\) と表現します。\(\langle100\rangle\) は単一のベクトルを意味しているのではなく、 \([100]\) を含む等価なベクトルの集合という意味です。当然ながら山括弧が使われるのは、物体の対称性が限定されている文脈に限られます。
もう一つ結晶の方向や距離を表現する概念として、「結晶面」があります。これについては「5.1. 結晶面と回折」で改めて説明します。
結晶系
結晶系 (crystal system) とは、結晶の分類方法の一つであり、結晶の持つ並進以外の対称性と両立しうる形状という観点で分類されています。この分類方法を正確に理解するためには空間群の知識が必要であるため、その議論は後回しにして、とりあえず3次元の結晶系は次のように分類されるということで読み進めてください。
| 結晶系 | 三斜晶系 | 単斜晶系 | 直方晶系 | 三方晶系 六方晶系 | 正方晶系 | 立方晶系 |
| 説明 | 3辺は直交しない | 3辺のうち1辺 (\(b\)) が残り2辺と直交する | 3辺は互いに直交する | 2辺 (\(a,b\)) は120°で交わり長さが等しく、残り1辺 (\(c\)) と直交する | 3辺は直交し、そのうち2辺 (\(a,b\)) の長さは等しい | 3辺は直交し、長さはすべて等しい |
| 模式図 |  | 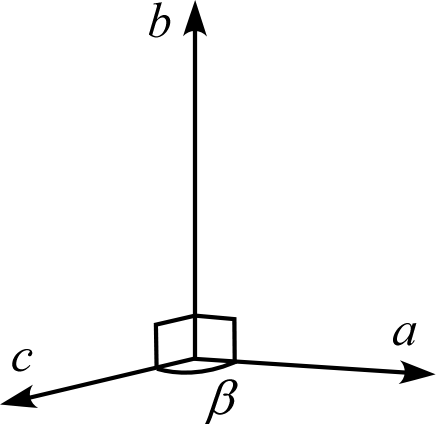 | 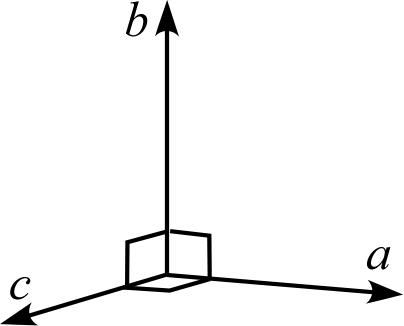 | 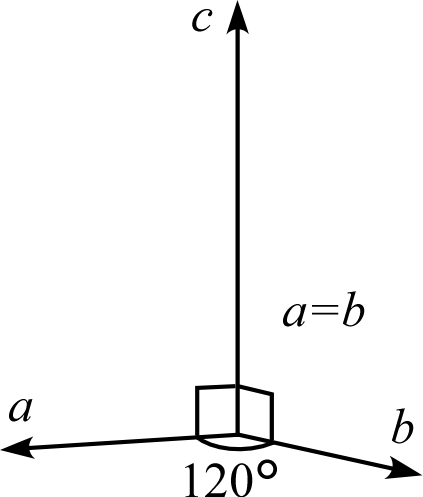 | 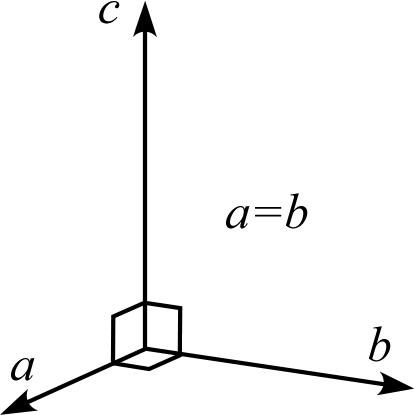 | 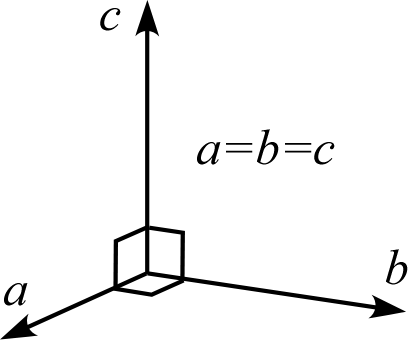 |
| ユニークな対称要素5 | \(1\)あるいは\(\bar{1}\) | \(2\)あるいは\(m\ (=\bar{2})\) | 3つの方向に\(2\)あるいは\(m\ (=\bar{2})\) | \(3\) あるいは \(6\) | \(4\) あるいは \(\bar{4}\) | 4つの方向に\(3\) |
各結晶系にはその結晶系を特徴づけるユニークな対称要素 (回転軸や回反軸) が存在し、その方向を主軸といいます。ユニークな対称要素が二つ以上ある場合は、二つ目以降を副軸とよびます。この話題については、「2.2. 点群と空間群の記法」で改めて取り上げます。
ここでは、結晶系に関するいくつかのトリビアなトピックを紹介します。
二斜晶系はなぜないのか
なぜ三斜晶系と単斜晶系があるのに、「二斜晶系」はないのでしょうか?「二斜晶系」を言葉通り解釈すれば、αは90°だがβやγは90°ではない、という単位格子ですね。このような平行六面体は、一見すると三斜晶系の場合と比べて対称性が高くなったように感じるかもしれません。しかしよく考えると、この形状を不変に保つ操作は1回転あるいは1回反のみであり、2以上の次数の回転・回反操作は許されません。つまり、対称性という観点からは三斜晶系と同じなのです。たまたまα=90°だったとしても、その結晶はあくまで三斜晶系です。
三方晶系と六方晶系の違い
同じ単位格子の形状なのになぜこの二つを分けなければいけないのか、不思議に感じたことはないでしょうか。別ページに詳しく書きましたので、ご覧になってください。
正方晶系・立方晶系と4回回転
正方晶系や立方晶系に属する結晶の形状について想像してみてください。「正方」とか「立方」という言葉が含まれますから、どうしても正方形や立方体的な形状、すなわち4回回転操作を含むような形状を思い浮かべてしまうのではないでしょうか。もちろんそういう結晶もあるのですが、全く正方形的な要素のない場合もあります。例えば、立方晶系に属する点群\(23\)の場合、次のような結晶形状が許されます。この結晶は6方向の(100)面(赤色)と4方向の(111)面(緑色)で囲まれた形状をしています。
正方晶系や立方晶系だからと言って4回回転操作を含むとは限らない、ということに注意しましょう。
単純格子と複合格子
はじめに、この節の図中の白丸◯は格子点を意味しており、原子のような具体的な物質が存在しているわけではないことにご注意ください。重要なのは格子点と格子点を結ぶ並進ベクトルの方向と距離です。
単位格子 (unit cell) とは空間中の独立な3つの並進ベクトルを三辺とするような平行六面体のことです。単純 (primitive) 格子とは、平行六面体の体積が最小となるように並進ベクトルを選んだ時の単位格子です。単純格子の各頂点は格子点であり、それ以外の格子点はありません。
一方、複合 (complex) 格子とは最小ではなくあえて大きな体積を選んだ単位格子のことです。複合格子の格子点は、各頂点に加えて、面の中心や格子の中心など存在します。なぜわざわざ大きな体積を選ぶのかといえば、「結晶系」で単位格子形状を分類することを優先し数学的な表現を簡潔にしたいからです6。
単純格子 (\(P\))
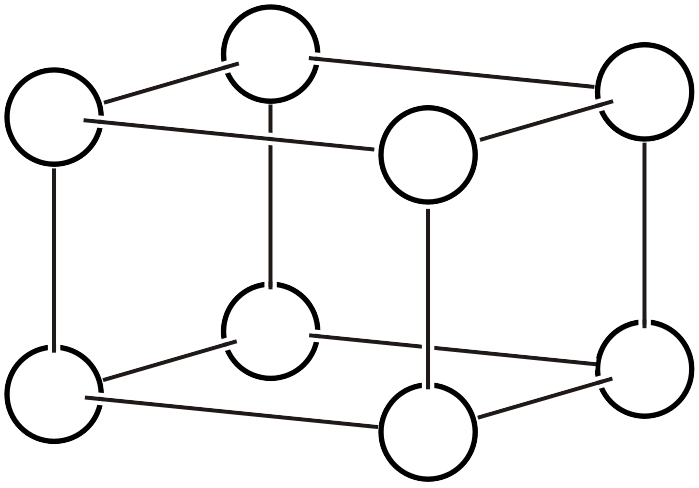
複合格子は結晶系を意識してあえて大きな体積を選んだ格子なわけですが、むやみに大きな体積をとってしまうとむしろ利便性が失われます。意味のある複合格子の取り方は、以下の四種類に限られます。
- 体心格子 (\(I\)) : 単位格子の中心に格子点が存在
- 底心格子 (\(A, B, C\)) : 単位格子のある面の中心に格子点が存在
- 面心格子(\(F\)): 単位格子の全て面の中心に格子点が存在
- 菱面格子(\(R\)): 単位格子の体対角線を三等分する位置に格子点が存在 (三方晶系のみ)
体心格子
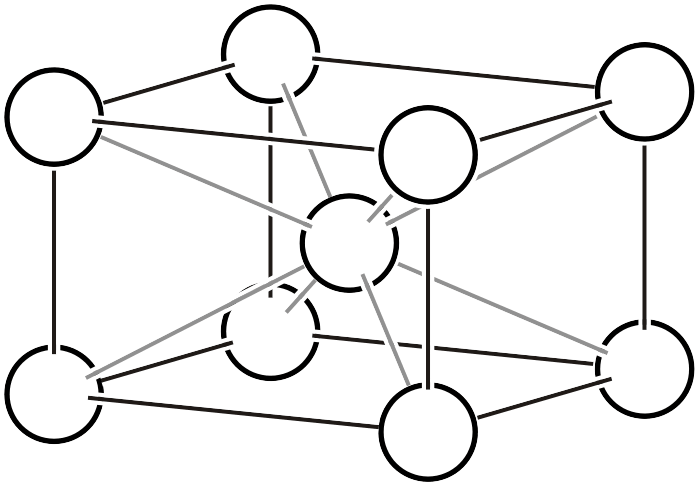
底心格子
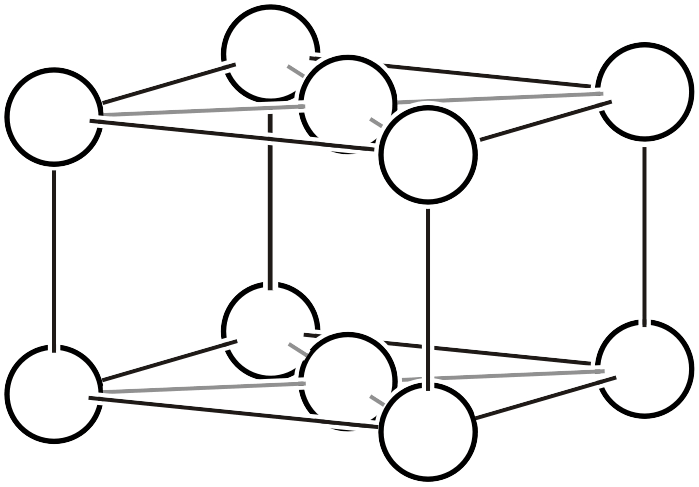
面心格子
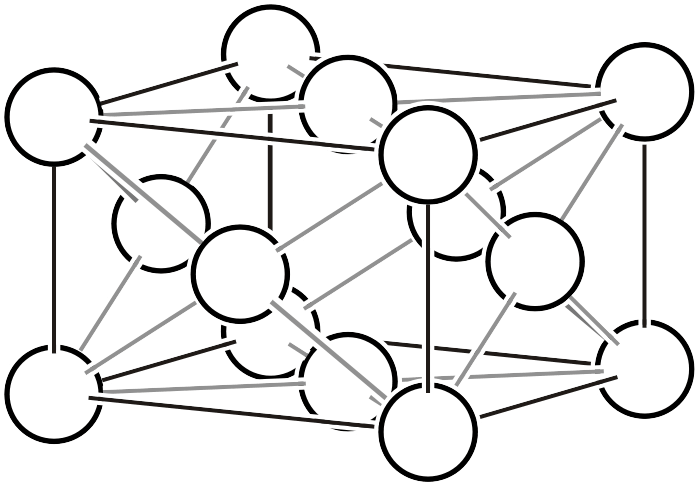
菱面格子

次に、それぞれの複合格子について単純格子との幾何学的関係を見ていきましょう。
体心格子 (\(I\)7)
体心格子は格子内に2つの格子点 (白丸)を含みます。左図では格子点が合計9つ描かれていますが、頂点の格子点がこの格子に寄与するのは1/8だけだと考えて下さい。また、格子点と原子の場所が一致するわけではないことにもご注意ください。体心格子はあえて大きく選んだ単位格子ですから、単純単位格子に変換できます。右図のように、体心格子を4つ並べ、濃黒線で示したような格子を選ぶと、体積が半分の単純単位格子になることが分かります。
体心格子

体心格子 ➡ 単純格子

底心格子 (\(A, B, C\))
底心格子は格子内に2つの格子点 (白丸)を含みます。左図のように、単位胞の六面のなかで、対となる二面のそれぞれの中心に格子点が存在します。右図のように、底心格子を2つ並べ、濃黒線で示したような格子を選ぶと、体積が半分の単純単位格子になることが分かります。
底心格子

底心格子 ➡ 単純格子
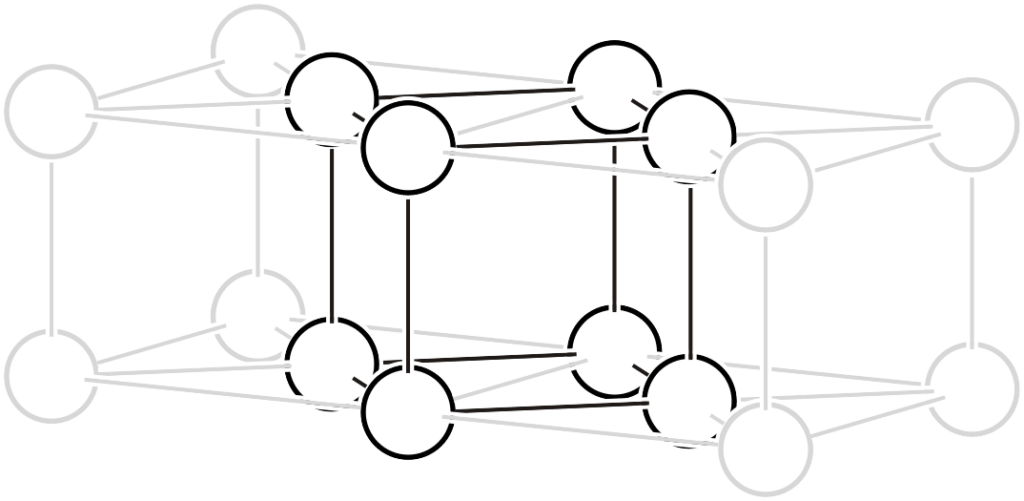
底心格子の記号には \(A, B, C\) の三種類があり、軸\(a,b,c\)との関係を表しています。例えば 底心格子\(A\)とは、\(b/2+c/2\)に格子点が存在することを表します。
面心格子 (\(F\))
面心格子は格子内に4つの格子点 (白丸)を含みます。左図のように、単位胞の全ての面の中心に格子点が存在します。右図のような濃黒線で示したような格子を選ぶと、体積が1/4の単純単位格子になることが分かります。
面心格子

面心格子 ➡ 単純格子
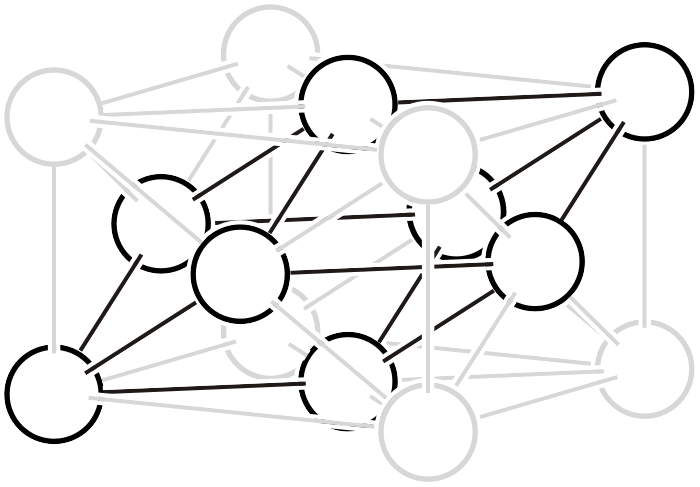
菱面格子 (\(R\))
菱面格子は一部の三方晶系に属する結晶に対して用いられる用語ですが、文脈によって意味合いが変わるので注意が必要です。単に菱面格子と言ったら 「三辺の長さと交わる角度が等しい単位格子 (\(a=b=c,\,\, \alpha=\beta=\gamma\))」 を意味することが多いのですが、ここでは「菱面格子系8」に分類される結晶に対して「六方格子設定 (\(a=b, \alpha=\beta=90°, \gamma=120°\))」で表現した単位格子という意味で使います。菱面六方格子と表現することもあります。
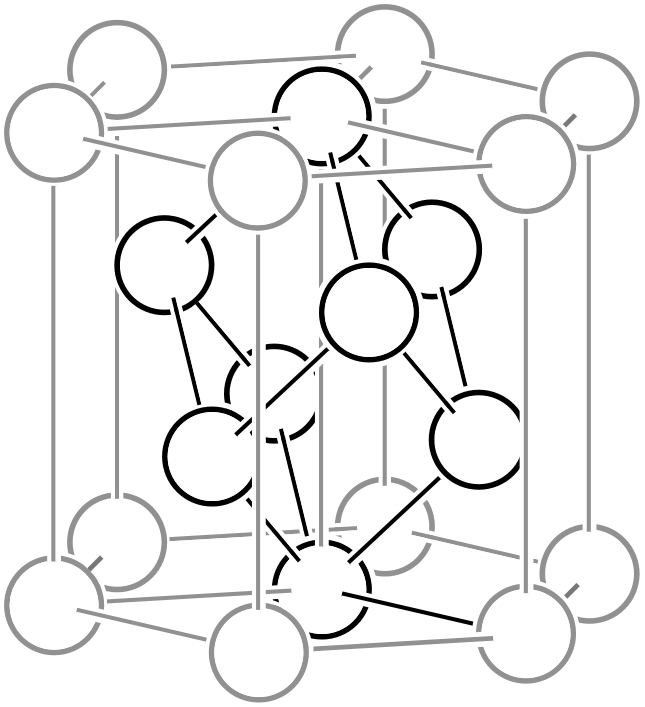
左図のように、単位格子の体対角線の方向を3等分する位置に格子点が存在し、格子内に3つの格子点 (白丸)を含むのが、菱面六方格子です。他の複合格子と同様に、菱面六方格子も格子をいくつか並べると単純格子に変換できます。まず、三方晶系は必ず\(3\)回回転軸を有していますので、中図のように120°ずつ回転した三つの菱面六方格子を並べてみましょう。三つの格子の中心に位置する格子点と、高さが1/3および2/3の位置にある格子点を全て結ぶと、体積が1/3の単純格子 (すなわち菱面格子系の菱面格子設定、あるいは単純菱面格子) に変換することができます。菱面格子の幾何学については、別ページの説明も併せてご覧ください。
菱面六方格子

120°の関係にある3つの菱面六方格子
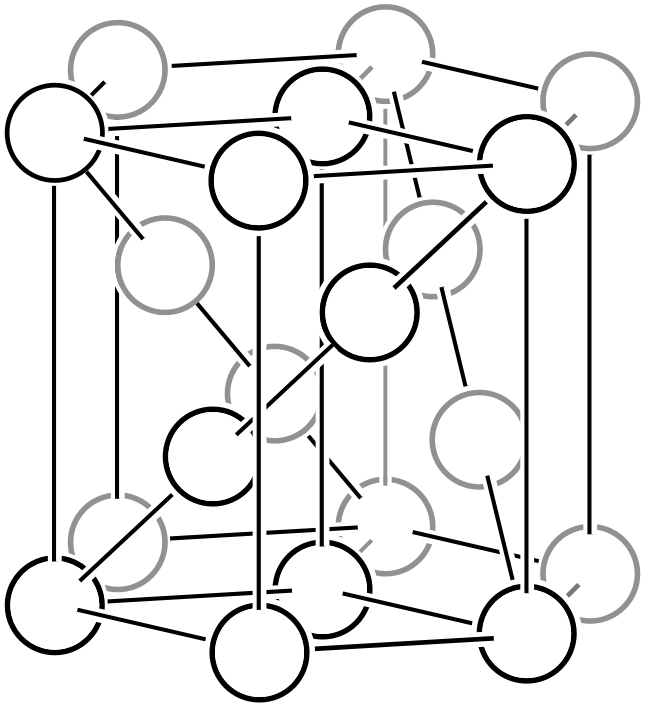
単純格子 (単純菱面格子)
ブラベー格子(Bravais lattice9)
格子点にのみ原子が存在するような結晶は、対称性の観点からいくつに分類できるか (同型ではない群はいくつあるか)? これがブラベー格子の概念です10。別の言い方をすると、すべての結晶系に対してすべての複合格子の要素を加えた空間格子から、より小さな単位格子を使っても対称性を失わないものや、基底ベクトルの変換によって等価な関係になるものを除いた空間格子のことです。これについても詳細な議論は改めて別ページで行いますので、とりあえず先に進みましょう。ブラベー格子は、2次元の場合は5種類、3次元の場合は14種類あります。歴史的には先にブラベー格子の概念が導かれ、そのあとに結晶系の分類が行われたのですが、ここでは結晶系ごとに各ブラベー格子 (3次元) を説明します。
三斜晶系
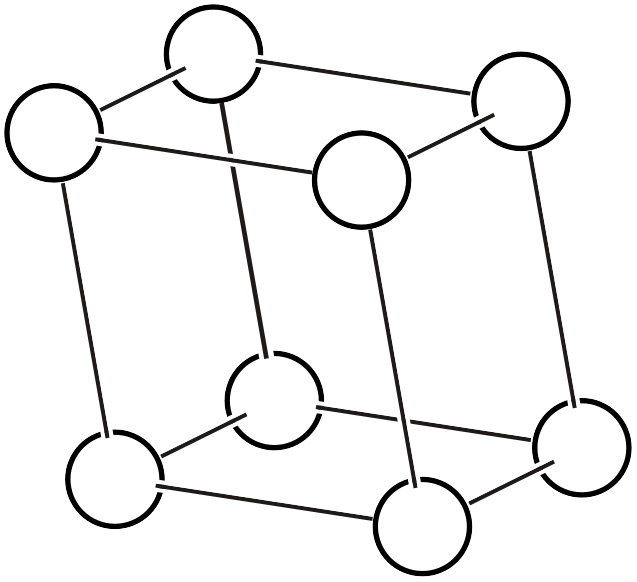
三斜晶系のブラベー格子には、単純格子しかありません。なぜなら、三斜晶系の並進を含まない対称操作(線形操作) は\(1\)あるいは\(\bar{1}\)のみであり、あえて体心格子や面心格子を取ったとしても全く旨味が無いのです。ただし、限定された状況(例えば相転移前後の単位格子形状を変えずに議論したい場合など)では、あえて体心格子や面心格子をとることもあります。

単純三斜格子 (\(aP\))
単斜晶系
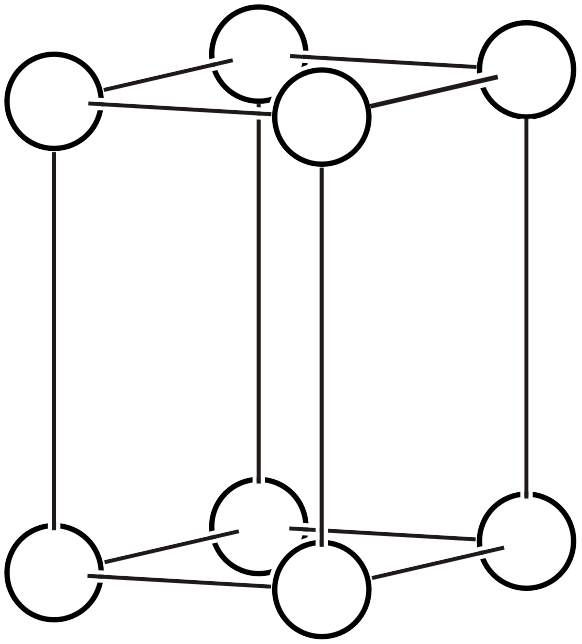
単斜晶系のブラベー格子は、通常は\(b\)軸を主軸として、単純格子と底心格子があります。体心格子や面心格子の単斜晶系は、適当な軸変換によって底心格子と等価になってしまうため、わざわざ分類することはしません。ただし、なんらかの事情があって、あえて別の軸を主軸としたり、底心格子ではなく体心格子を取ったりすることもあります。このような変換については別ページで説明しています。

単純単斜格子 (\(mP\))
底心単斜格子 (\(mC\))
直方晶系
直方晶系のブラベー格子は、単純格子、底心格子、体心格子、面心格子の全てがあります。

単純直方格子 (\(oP\))

体心直方格子 (\(oI\))

底心直方格子 (\(oC\))

面心直方格子 (\(oF\))

三方晶系, 六方晶系
三方晶系と六方晶系のブラベー格子は、\(c\)軸を主軸として、単純格子と菱面格子があります。菱面格子の幾何学については、別ページの説明もご覧ください。

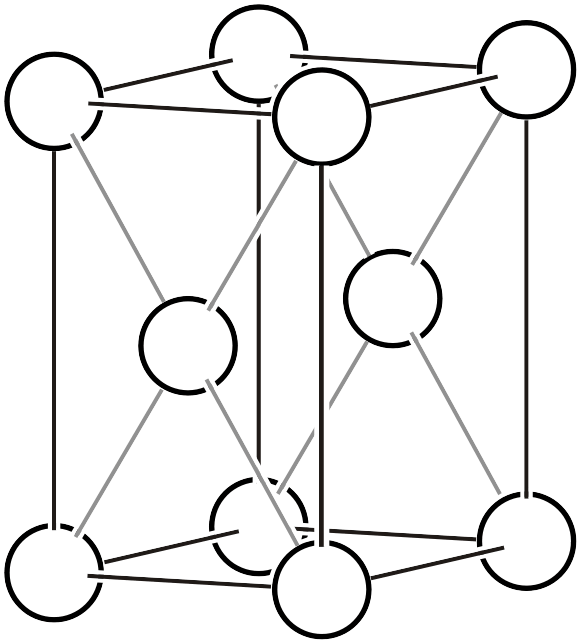
単純六方格子 (\(hP\))
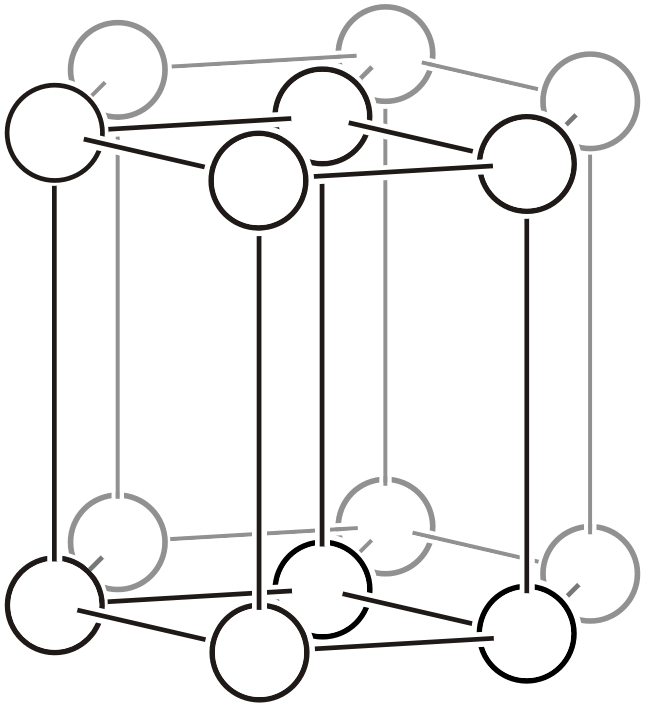
菱面六方格子 (\(hR\))
正方晶系
正方晶系のブラベー格子は、\(c\)軸を主軸として、単純格子と体心格子があります。底心正方格子は、単純正方格子と取り直すことができるので、分類されません。面心正方格子は、体心正方格子と取り直すことができるので、分類されません。

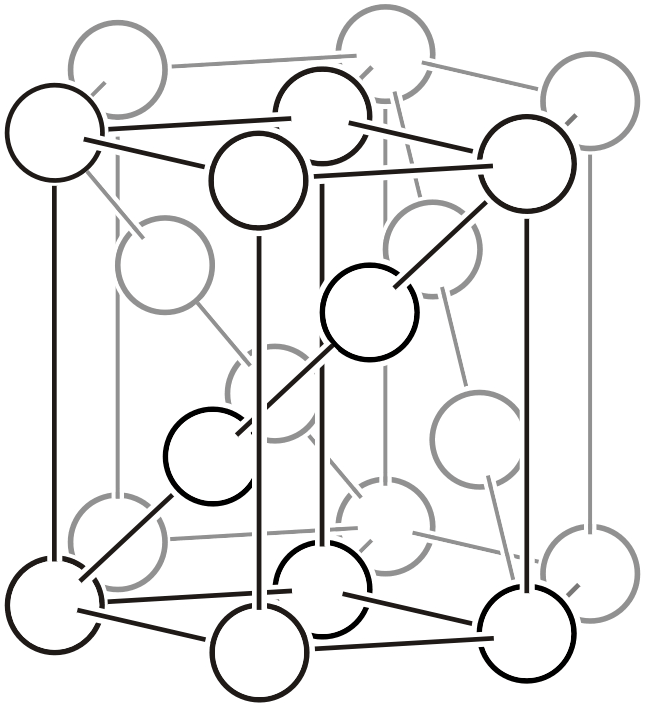
単純正方格子 (\(cP\))
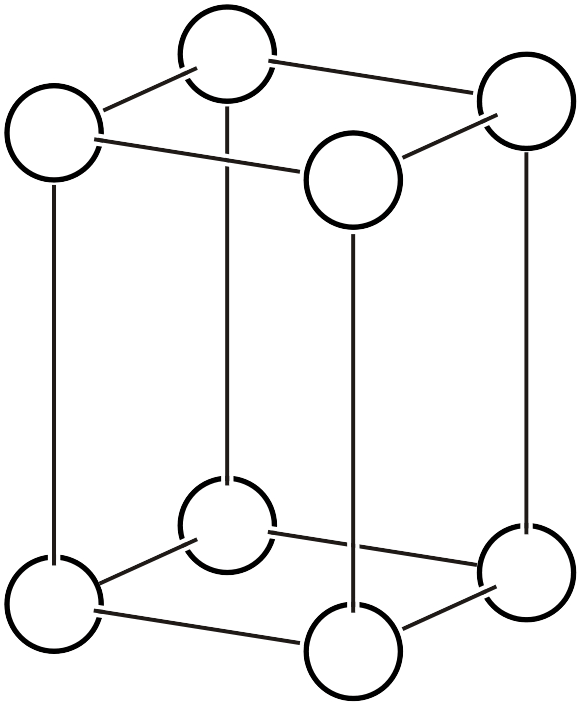
体心正方格子 (\(cI\))
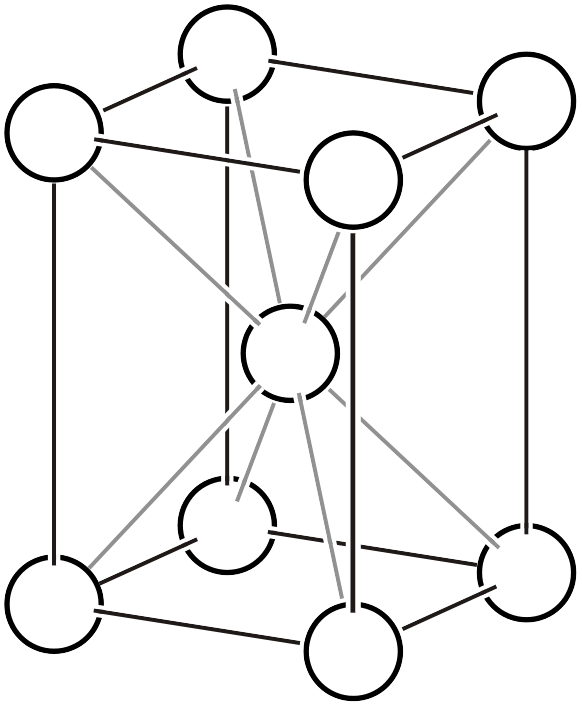
立方晶系
立方晶系のブラベー格子は、単純格子、体心格子、体心格子があります。底心立方格子は、[111]方向に存在する3回回転操作に反するため、存在しません。

単純立方格子 \cP\)
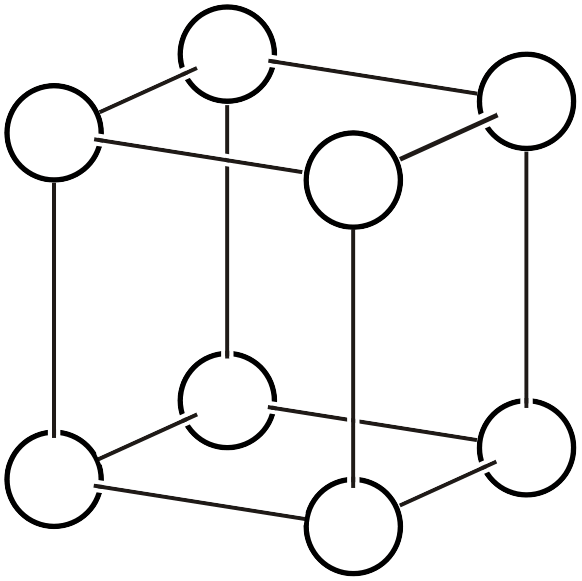
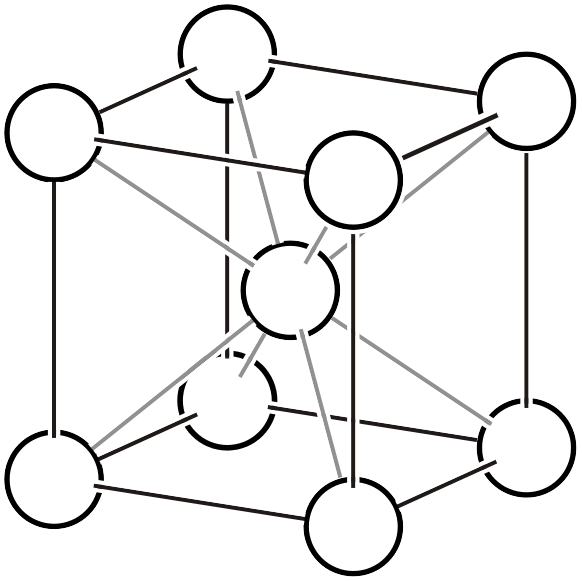
体心立方格子 \(cI\)
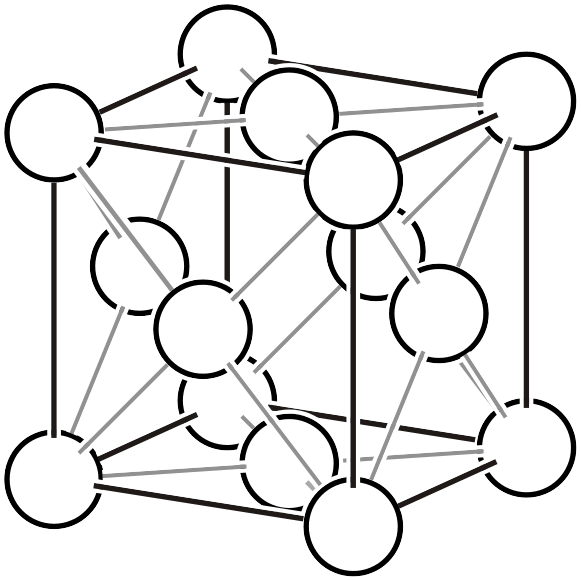
面心立方格子 \(cF\)
- この基準は、結晶学の業界でよく使われており事実上のデファクトスタンダードといってよいでしょう。 ↩︎
- 右手系と左手系の区別に気を付けましょう。ここでは右手系になるように計算しています。\(\mathbf{a}\)を反転させると、左手系に変換されます。 ↩︎
- 行列やベクトルの演算は、Excelでもできますし、Mathematicaのような数式処理ソフトやPythonのようなプログラミング言語とも親和性が高く、応用が利きます。 ↩︎
- 一見すると回反の記号のように見えますが、全く異なるので注意しましょう。 ↩︎
- ここでは、回転や回反のみを挙げていますが、実は映進やらせんもユニークな要素になり得ます。映進は、次数が2の回反 (=\(m\)) に並進が加わったものですから、\(m\)と同等の扱いです。らせんは、回転の次数がそのまま対応しますので、たとえば \(2_1\) らせん軸が三方向に存在する場合は直方晶系ということになります。 ↩︎
- もし複合単位格子の概念を導入しなかったら、例えば「2回回転軸が存在する結晶なのに直角柱形状の単位格子をとれない」といった状況が生じ、その結晶の構造や物性を理解する際に(不可能ではないものの)大変な労力を強いられることになります。 ↩︎
- ドイツ語 innenzentriert (内部中心)に由来します。英語だったら body centered となるので “B” の文字を使ってほしいところですが、そうすると底心格子をあらわす記号とかぶってしまうのです。 ↩︎
- 格子系については「3.7. 空間群の分類」をご覧ください。 ↩︎
- 19世紀のフランスの結晶学者であるAuguste Bravaisの名前にちなんでいます。 ↩︎
- この意味で図中の白丸◯は格子点ではなく原子と考えても構わないのですが、ブラベー格子の概念の重要性は「格子点にのみ原子が存在するような結晶」そのもではなく、すべての結晶をブラベー格子に対応付ける分類 (ブラベー代数的類)にあります。詳しい説明は「3.7. 空間群の分類」で行います。 ↩︎