格子定数と結晶幾何学
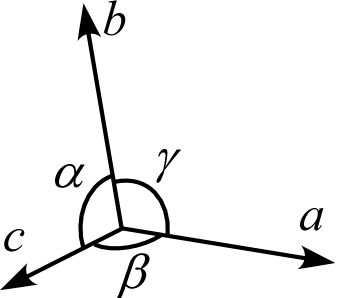
3次元の結晶の単位格子は、通常3方向の並進ベクトル \(\textbf{a}, \textbf{b}, \textbf{c}\) のそれぞれの長さ\(a,b,c\) と、それらの間の角度 \(\alpha,\beta,\gamma\) によって表現します。これら \(a,b,c,\alpha,\beta,\gamma\) の6つのパラメータを(実単位)格子定数といいます1。立方晶系の場合を除いて、\(a,b,c\) は等しいとは限りませんし \(\alpha,\beta,\gamma\) が \(90^\circ\) とも限らないことに注意しましょう。格子定数を使えば、以下の様々な幾何学量を計算することが出来ます。
単位格子の体積 \(V\)
$$V=\sqrt{ a^2 b^2 c^2 (1-\cos^2{\alpha}-\cos^2\beta – \cos^2\gamma + 2 \cos\alpha \cos\beta \cos\gamma)}$$
\((hkl)\)面の面間隔 \(d\)
$$d =\sqrt{ V^2/(h^2 σ_{11} + k^2 σ_{22} + l^2 σ_{33} + 2 k l σ_{23} + 2 l h σ_{31} + 2 h k σ_{12})}
$$ ただし、\(σ_{11}= b^2 c^2 \sin^2\alpha,\ \ σ_{22}= c^2 a^2 \sin^2\beta,\ \ σ_{33}= a^2 b^2 \sin^2\gamma\)
\(σ_{23}= a^2 b c (\cos\beta \cos\gamma – \cos\alpha ),\ \ σ_{31}= a b^2 c (\cos\gamma \cos\alpha – \cos\beta ),\ \ σ_{12}= a b c^2 (\cos\alpha \cos\beta – \cos\gamma)\)
\((h_1k_1l_1)\) と \((h_2k_2l_2)\) のなす角 \(\theta\)
$$\cos\theta = d_1 d_2 \frac{h_1 h_2 σ_{11}+ k_1 k_2 σ_{22} + l_1 l_2 σ_{33} + (k_1 l_2 + k_2 l_1) σ_{23} + (l_1 h_2 + l_2 h_1 ) σ_{31}+ (h_1 k_2 + h_2 k_1 ) σ_{12}} { V^2}
$$ ただし、 \(d_1, d_2\) は それぞれ \((h_1k_1l_1)\) と \((h_2k_2l_2)\) の面間隔
\([uvw]\) 軸の長さ \(r\)
$$r =\sqrt{ u^2 a^2 + v^2 b^2 + w^2 c^2 + 2 v w b c \cos\alpha+ 2 w u c a \cos\beta + 2 u v a b \cos\gamma}$$
\([u_1v_1w_1]\) 軸と \([u_2v_2w_2]\) 軸のなす角 \(\psi\)
$$\cos\psi = \frac{u_1 u_2 a^2 + v_1 v_2 b^2 + w_1 w_2 c^2 + (v_1 w_2 + v_2 w_1) b c \cos\alpha + (w_1 u_2 + w_2 u_1) c a \cos\beta +(u_1 v_2 + u_2 v_1) a b \cos\gamma}{ r_1 r_2}
$$ ただし、 \(r_1, r_2\) はそれぞれ [\(u_1v_1w_1\)] と [\(u_2v_2w_2\)] の軸の長さ
\((hkl)\) 面法線と \([uvw]\) 軸のなす角 \(\phi\)
$$\cos\phi = (h u + k v + l w) d / r$$
さて、ここまで複雑な式をつらつらと書いてきましたが、実は次に述べる逆格子の概念とベクトルを利用すると、上記のような幾何学量をもっと簡単かつ直感的に表現できます。
実格子と逆格子
逆行列と逆格子の定義
実単位格子ベクトル \(\textbf{a}, \textbf{b}, \textbf{c}\) に対して、逆単位格子ベクトル \(\mathbf{a^*}, \mathbf{b^*}, \mathbf{c^*}\)とは以下のように定義されるベクトルのことです (念のため、\(\mathbf{^*}\) はかけ算ではなく添え字です)。$$
\mathbf{a^*}=\frac{\textbf{b}\times\textbf{c}}{V},\ \ \mathbf{b^*}=\frac{\textbf{c}\times\textbf{a}}{V},\ \ \mathbf{c^*}=\frac{\textbf{a}\times\textbf{b}}{V}
$$ここで \(V\) は(実)単位格子の体積です。また \(\times\) はベクトルの外積を表します。
この関係は、行列表現で定義することもできます。まず、実単位格子ベクトル \(\textbf{a}, \textbf{b}, \textbf{c}\) を直交座標系で成分表示して\((a_x, a_y, a_z)、(b_x, b_y, b_z)、(c_x, c_y, c_z) \)とします。これらを行成分として以下のような3×3行列 \(R\) をつくり、次いでその逆行列 \(R^{-1}\) を計算2しましょう。
$$R =\begin{pmatrix}a_x & a_y & a_z \\b_x & b_y & b_z \\c_x & c_y & c_z\end{pmatrix}
\ \ \Longrightarrow \ \ \
R^{-1} =\begin{pmatrix}a^*_x & b^*_x & c^*_x \\ a^*_y & b^*_y & c^*_y \\ a^*_z & b^*_z & c^*_z \end{pmatrix}
$$この時、\(R^{-1}\) の列成分は逆単位格子ベクトルに対応します。
$$\textbf{a}^*=(a^*_x,a^*_y,a^*_z),\ \ \textbf{b}^*=(b^*_x,b^*_y,b^*_z),\ \ \textbf{c}^*=(c^*_x,c^*_y,c^*_z)
$$ 実単位格子ベクトルと逆単位格子ベクトルには以下のような関係があります (これを定義と考えてもかまいません)。
$$ \mathbf{a} \mathbf{a^*} = \mathbf{b} \mathbf{b^*} = \mathbf{c} \mathbf{c^*} = 1,\\
\mathbf{a} \mathbf{b^*} = \mathbf{a} \mathbf{c^*} = \mathbf{b} \mathbf{c^*} = \mathbf{b} \mathbf{a^*}= \mathbf{c} \mathbf{a^*}= \mathbf{c} \mathbf{b^*} =0$$
逆格子ベクトルの性質
一旦逆単位格子ベクトルが求まれば、任意の\((hkl)\) 面の面間隔や面間の角度などをベクトル演算で容易にもとめることができます。なぜなら、\((hkl)\) 面に対応する次の逆格子ベクトル$$
\textbf{g} = h \textbf{a}^* + k \textbf{b}^* + l \textbf{c}^*
$$はそのベクトルの長さが面間隔 \(d\) の逆数を意味しており方向は法線の方向を意味するからです。例えば \((hkl)\) 面の面間隔 \(d\) は $$
d = 1/|\textbf{g}|,\ \ \ where\ \ \ \textbf{g}= h \textbf{a}^* + k \textbf{b}^* + l \textbf{c}^*
$$ですし、\((h_1k_1l_1)\)と\((h_2k_2l_2)\)の面間角度 \(\theta\) は$$
\cos\theta = \frac{\mathbf{g_1 g_2}}{|\mathbf{g_1}| |\mathbf{g_2}|},\ \ \ where\ \ \ \mathbf{g_1}= h_1 \textbf{a}^* + k_1 \textbf{b}^* + l_1 \textbf{c}^*\ \ \ \&\ \ \ \mathbf{g_2} = h_2 \textbf{a}^* + k_2 \textbf{b}^* + l_2 \textbf{c}^*$$ という計算で容易に求まります。複雑な三角関数を使う必要はありません。幸せになれますね。
格子定数からベクトルへの変換
さて、上ではさらっと 「実単位格子ベクトルを直交座標系で成分表示する」 と書きましたが、具体的にどのように計算をしたらよいでしょう。3つの実単位格子ベクトル \(\mathbf{a}, \mathbf{b}, \mathbf{c}\) は直交するとは限りませんから、それぞれを直交座標系の \(X,Y,Z\) 軸に一致させることは一般的には不可能です。\(\mathbf{a}\) を \(X\) 軸に一致させたい人もいれば、\(\mathbf{c}\) を \(Z\) 軸に一致させたい人もいるでしょう。1つの軸の方向を決めたとて、まだ自由度は残ります。当然ながら万人が納得する唯一の正解はありません。ここでは、以下のような基準3で、(実単位)格子定数 \(a,b,c,\alpha,\beta,\gamma\) を直交座標系で成分表示する方法を説明しましょう。
- \(\mathbf{c}\) を \(Z\) 軸に一致させる
- \(\mathbf{b}\) を \(YZ\) 平面上に一致させる
この基準に従えば、まず \(\mathbf{c}\) については
$$ \mathbf{c} = (0,0,c)
$$と簡単に定義できます。次に \(\mathbf{b}\) については \(\mathbf{c}\) とのなす角が \(\alpha\) であることと \(YZ\) 平面に一致する (すなわち \(X=0\) である) ことを考慮して、
$$ \mathbf{b} = (0,b \sin\alpha,b \cos\alpha)
$$とやはり簡単に定義できます。\(\mathbf{a}\) についてはちょっと複雑になりますが、すでに求まっている \(\mathbf{b, c}\) との関係を考慮すれば、
$$ \mathbf{a} = (a \sqrt{1-\cos^2\beta-\left(\frac{\cos\gamma-\cos\alpha \cos\beta}{\sin\alpha}\right)^2},\ \ a \frac{\cos\gamma-\cos\alpha \cos\beta}{\sin\alpha},\ \ a\cos\beta)
$$となります4。以上のように \(\mathbf{a}, \mathbf{b}, \mathbf{c}\) を計算すれば、後は簡単なベクトル・行列の演算で逆単位格子ベクトルも求まりますし、さらにそれらを使って面間隔や面間の角度なども容易に計算できます5。
実単位格子定数と逆単位格子定数の関係
蛇足の情報です。実空間の格子定数を(ベクトルではなく) \(a, b, c, \alpha, \beta, \gamma\) とした時、逆空間の格子定数 \(a^*, b^*, c^*, \alpha^*, \beta^*, \gamma^*\) は次のように変換できます。
$$\begin{array}{rcl}
a^* & = & (b c \sin\alpha)/v\\
b^* & = & (c a \sin\beta)/v, \\
c^* & = & (a b \sin\gamma)/v \\
\cos\alpha^* & = &(\cos\beta \cos\gamma -\cos\alpha)/(\sin\beta \sin\gamma)\\
\cos\beta^* &=& (\cos\gamma \cos\alpha -\cos\beta)/(\sin\gamma \sin\alpha)\\
\cos\gamma^* &=& (\cos\alpha \cos\beta -\cos\gamma)/(\sin\alpha \sin\beta)
\end{array}$$
逆空間格子の体積 \( v^*\) は、
$${v^*}^2={a^*}^2 {b^*}^2 {c^*}^2 (1-\cos^2\alpha^*-\cos^2\beta^*-\cos^2\gamma^* +2 \cos\alpha^* \cos\beta^* \cos\gamma^*)
$$という計算で求められます。 \(v^*\) と実空間格子の体積 \( v\) には \(v^*=1/v\) の関係があります。このほかにも様々な関係式があります6が、コンピュータが発達した現在、上述の逆単位格子ベクトルの概念を利用したほうがほとんどの場合シンプルに問題解決できるでしょう。
脚注
- このページでは、「逆単位格子定数」という概念も出てきますので、あえて冗長に「実単位格子定数」と表現しています。普通の文脈では「格子定数」と表現して構いません。 ↩︎
- ちなみに3×3行列の逆行列は公式があって
$$R^{-1} =
(-a_z b_y c_x + a_y b_z c_x + a_z b_x c_y – a_x b_z c_y – a_y b_x c_z + a_x b_y c_z)^{-1}
\begin{pmatrix}
-b_z c_y + b_y c_z & +a_z c_y – a_y c_z & -a_z b_y + a_y b_z \\
+b_z c_x – b_x c_z & -a_z c_x + a_x c_z & +a_z b_x – a_x bz \\
-b_y c_x + b_x c_y & +a_y c_x – a_x c_y & -a_y b_x + a_x b_y
\end{pmatrix}
$$という式を使って解くことが出来ます。 ↩︎ - この基準は、結晶学の業界でよく使われており事実上のデファクトスタンダードといってよいでしょう。 ↩︎
- 右手系と左手系の区別に気を付けましょう。ここでは右手系になるように計算しています。\(\mathbf{a}\)を反転させると、左手系に変換されます。 ↩︎
- 行列やベクトルの演算は、Excelでもできますし、Mathematicaのような数式処理ソフトやPythonのようなプログラミング言語とも親和性が高く、応用が利きます。 ↩︎
- 逆格子定数を組み合わせて以下のように \(A,B,C,U,V,W\) を定義します。
\( A={a^*}^2,\ \ B={b^*}^2,\ \ C={c^*}^2,\ \ U=2b^*c^*\cos\alpha^*,\ \ V=2c^*a^*\cos\beta^*,\ \ W=2a^*b^*\cos\gamma^*\)
逆単位格子の体積 \({v^*}\) は以下のように表現できます。
\({v^*}^2= (4ABC-AU^2-BV^2-CW^2+UVW)/4\)
ある結晶面 \((h k l)\) の面間隔を \( d\) は以下のように表現できます。
\(\frac{1}{d^2} = h^2 A + k^2 B + l^2 C + kl U + lh V + hk W \)
以下は蛇足の蛇足な関係式です。使う場面はあまりないでしょう。
\(a^* = \sqrt{A}, \ b^* = \sqrt{B}, \ c^* = \sqrt{C}\)
\( \alpha^* =\arccos \frac{U}{2 \sqrt{BC}}, \ \beta^* = \arccos \frac{V}{2 \sqrt{CA}}, \ \gamma^* =\arccos \frac{W}{2 \sqrt{AB}} \)
\( a = \frac{b^* c^* \sin{\alpha^*}}{v^*} = \left(\frac{4BC-U^2 }{4ABC-AU^2-BV^2-CW^2+UVW}\right)^{1/2} = \left(A-\frac{BV^2+CW^2-UVW}{4BC- U^2}\right)^{-1/2} \)
\( b = \frac{c^* a^* \sin{\beta^*}}{v^*} = \left(\frac{4CA-V^2 }{4ABC-AU^2-BV^2-CW^2+UVW}\right)^{1/2} = \left(B-\frac{CW^2+AU^2-UVW}{4CA- V^2}\right)^{-1/2} \)
\( c = \frac{a^* b^* \sin{\gamma^*}}{v^*} = \left(\frac{4AB-W^2 }{4ABC-AU^2-BV^2-CW^2+UVW}\right)^{1/2} = \left(C-\frac{AU^2+BV^2-UVW}{4AB- W^2}\right)^{-1/2} \)
\(\sin\alpha = {\frac{a^*}{bc v^*}} = \left( \frac{4A(4ABC-AU^2-BV^2-CW^2+UVW)}{(4CA-V^2)(4AB-W^2)}\right)^{1/2} =\left( 1- \frac{(VW-2AU)^2}{(4CA-V^2)(4AB-W^2)} \right)^{1/2} \)
\(\sin\beta = {\frac{b^*}{ca v^*}} = \left( \frac{4B(4ABC-AU^2-BV^2-CW^2+UVW)}{(4AB-W^2)(4BC-U^2)}\right)^{1/2} =\left( 1- \frac{(WU-2BV)^2}{(4AB-W^2)(4BC-U^2)} \right)^{1/2} \)
\(\sin\gamma = {\frac{c^*}{ab v^*}} = \left( \frac{4C(4ABC-AU^2-BV^2-CW^2+UVW)}{(4BC-U^2)(4CA-V^2)}\right)^{1/2} =\left( 1- \frac{(UV-2CW)^2}{(4BC-U^2)(4CA-V^2)} \right)^{1/2} \)
\(\cos\alpha = \frac{\cos\beta^* \cos\gamma^* -\cos\alpha^* }{\sin\beta^* \sin\gamma^* } = \frac{VW-2AU}{\sqrt{(4CA-V^2)(4AB-W^2)} } \)
\(\cos\beta = \frac{\cos\gamma^* \cos\alpha^* -\cos\beta^* }{\sin\gamma^* \sin\alpha^* } = \frac{WU-2BV}{\sqrt{(4AB-W^2)(4BC-U^2)} } \)
\(\cos\gamma = \frac{\cos\alpha^* \cos\beta^* -\cos\gamma^* }{\sin\alpha^* \sin\beta^* } = \frac{UV-2CW}{\sqrt{(4BC-U^2)(4CA-V^2)} }\) ↩︎