実空間とは我々が通常認識しているような、長さの次元を持つ空間のことです。一方、逆空間とは実空間の周期性を反映した空間であり、長さの逆数の次元を持ちます。逆空間には特異点である原点が存在し1、原点からの方向と距離が実空間における周期性の方向と波長に対応します。
フーリエ変換
実空間と逆空間の関係は、数学的にはフーリエ変換にほかなりません。ある1次元の関数 \(f(x)\) とそれをフーリエ変換して得られる関数 \(g(u)\) には以下のような関係があります。 $$
g(u) = \int^{\infty}_{-\infty}f(x)\exp(-2\pi i x u) dx
$$ 2次元の場合は以下のようになります。$$
g(u,v) = \int^{\infty}_{-\infty}\int^{\infty}_{-\infty}f(x,y)\exp(-2\pi i [x u +y v]) dx
$$ 3次元にしたい場合は、さらに\(z\)や\(w\)の記号を加えて拡張してください。 いずれにしても、\(f\)が実空間 (における何かの量2をあらわす関数) であれば、\(g\) はその逆空間に対応します。
回折格子
さて、このようなフーリエ変換の数式だけを示されても多くの人にはピンとこないと思います。ここでは、もう少し直観的に逆空間の理解を深めるような説明していきたいと思います。実際に実空間と逆空間を対応付ける簡単な実験があります。それは以下に示すような 「回折格子」 の実験です。
回折格子には無数の穴が開いています。この穴の配置を「格子パターン」と呼ぶことにします。回折格子に向けて、穴の間隔より十分短い波長の光を当てると、穴を通過した光は互いに干渉を起こします。そして回折格子から十分離れた場所でこの干渉した光の模様を撮影します。この模様を「回折パターン」と呼ぶことにします。もう言わずもがなですね。そうです、格子パターンを実空間と見たとき、回折パターンがその逆空間に対応3するのです。この素晴らしい実験の背景や意味はWikipediaでも見てもらうことにして、以降は具体的にどのような格子パターンからどのような回折パターンが生まれるか、例を示していきましょう。
例1: 完全結晶の場合
格子パターン (実空間)

回折パターン (逆空間)

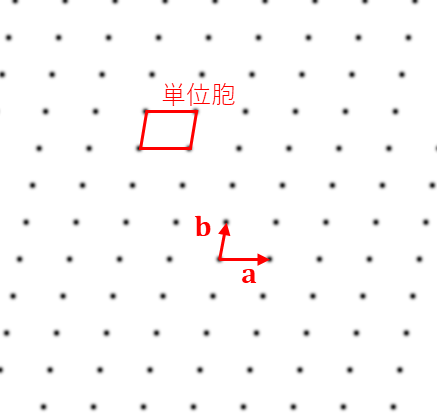
最初の例は、格子パターンが全く乱れのない周期性を持つ二次元結晶の場合です。念のため黒い点が光を通す穴です。このような格子パターンに光を当てると、右のような回折パターンが得られます。中心のスポットは光がそのまま直進した透過スポットであり、逆空間における原点に対応します。透過スポットの周りにみられるたくさんの点は、全て回折スポットです。回折スポットは周期的に並んでおり、透過スポットから離れると強度が弱くなっていきます。実空間における格子模様と逆空間における格子模様は、前のページで説明した実単位格子ベクトルと逆単位格子ベクトルの関係に対応しています。二次元の場合、実単位格子ベクトル\(\bf{a}, \bf{b}\) と逆単位格子ベクトル\(\bf{a^*}, \bf{b^*}\) の関係は以下のようになります。
格子パターン (実空間)
回折パターン (逆空間)
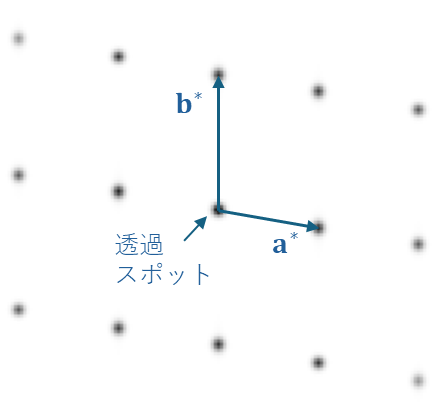
実単位格子ベクトルと逆単位格子 ベクトルの関係
$$\bf{a} \bf{a^*}=1\\
\bf{a} \bf{b^*}=0\\
\bf{b} \bf{a^*}=0\\
\bf{b} \bf{b^*}=1$$
\(\bf{a^*}\) は \(\bf{b}\)と直交し、かつ\(\bf{a}\)との内積が \(1\) になるようなベクトルです。同様に\(\bf{b^*}\) は \(\bf{a}\)と直交し、かつ\(\bf{b}\)との内積が \(1\) のベクトルです。回折パターンには、この逆格子ベクトルの幾何学に対応する図形が現れているのです。
例2: 積層欠陥がある場合
次の例は、単位胞は直上の例と同じですが、積層欠陥がランダムに存在する場合です。
格子パターン (実空間) (\(\frac{1}{2}\bf{a}\) along \(\bf{b^*}\))

回折パターン (逆空間)

不思議な回折パターンが生まれていますね。どの面がどの方向にどれくらいの量ずれた積層欠陥なのか、すぐわかった方は大変優秀です。上の格子パターンに単位胞の補助線を加えたのが以下の図です。\(\bf{b^*}\) に対応する面が、\(\bf{a}\) 軸方向に1/2ずれるような積層欠陥がランダムに存在していることがお分かりになるでしょうか。このような積層欠陥が生じると、回折スポットにも乱れが生じスポット状の強度分布と線状の強度分布が交互に現れるのです。
格子パターン (実空間) (\(\frac{1}{2}\bf{a}\) along \(\bf{b^*}\))

回折パターン (逆空間)
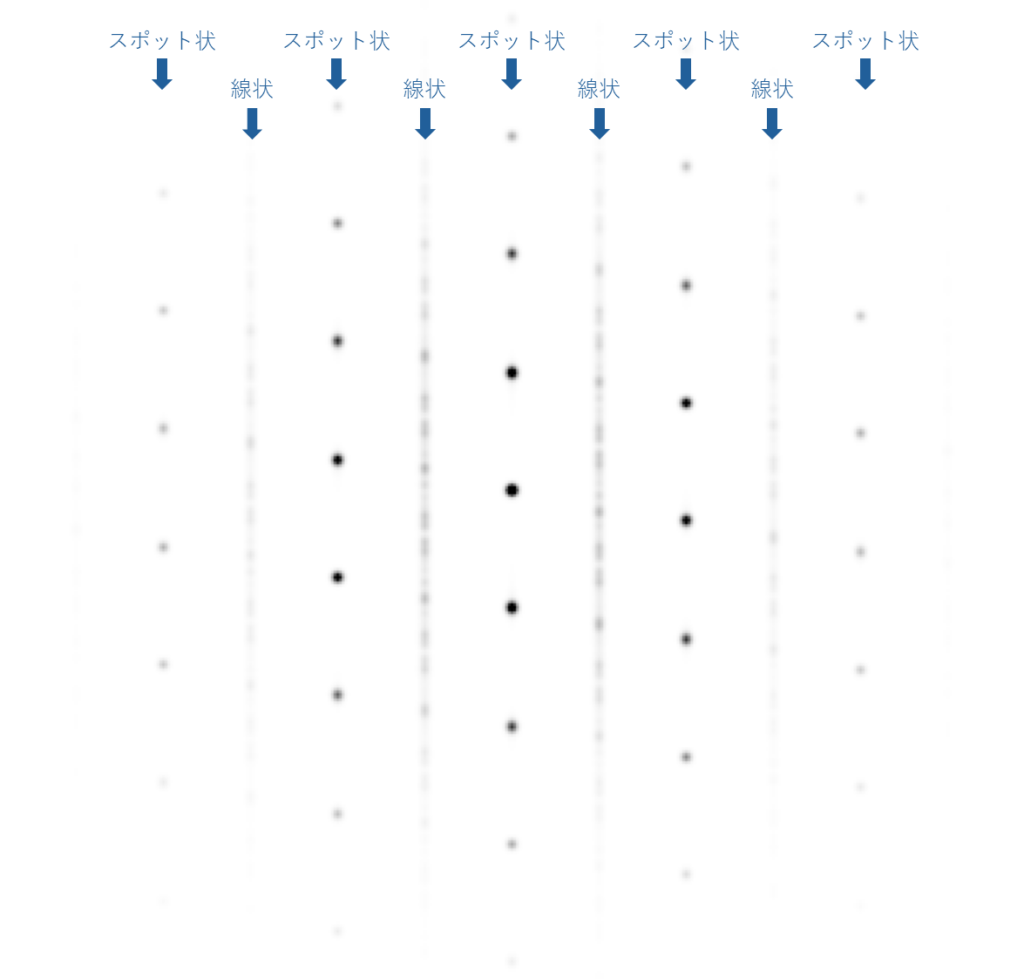
以下の図はずれの量が1/3の場合です。今度は回折パターン中の強度分布がスポット状→線状→線状→スポット状→… という周期になっていることにご注意ください。
格子パターン (実空間) (\(\frac{1}{3}\bf{a}\) along \(\bf{b^*}\))

回折パターン (逆空間)

例3 超構造、変調構造がある場合
今度は、超構造や変調構造の例を見ていきましょう。
以下は、穴の配置は完全結晶の場合と全く同じだが、穴の大きさに違いがあるような例です。大きい穴の列と小さい穴の列が上下方向に4倍の周期で繰り返しています。別の表現をすると、完全結晶の単位胞 (ここでは基本単位胞と呼びます) に対して、 \(\bf{b}\) 軸が4倍に伸びた単位胞をもつ結晶です。このような、基本単位胞の軸を整数倍した構造を、「超構造」 (super structure) といいます4。 \(\bf{b}\) 軸が4倍に伸びたら \(\bf{b^*}\) の長さは1/4になりますから、右のような回折パターンが得られるのです。ただし、基本的な穴の配置は完全結晶と同じであり、そのため基本単位胞に対応する回折スポット (ここでは基本スポットと呼びます) の強度が強くなっていることにもご注意ください。
格子パターン (実空間) (振幅変調 \(\bf{b’} = 4\bf{b}\))

回折パターン (逆空間)

さて、上の例は正確に「4倍」周期だったのですが、これが非整数倍になることもあります。このような構造を「変調構造」 (modulated structure) といいます。広い意味では、超構造も変調構造の一種です。以下は、 \(\bf{b}\) 軸を 6.28 倍に変調した例です。基本スポットの周りに弱いスポットが見られ、それらは基本スポットを整数で分割していません。
格子パターン (実空間) (振幅変調 \(\bf{b’} = 6.28\bf{b}\))

回折パターン (逆空間)

以上の二つの例は、穴の大きさの違いによる超構造あるいは変調構造でした。穴の大きさは、回折格子実験の場合は光の透過量に対応しますが、一般的な回折実験に拡張して考えると原子やイオンの散乱能 (scattering factor あるいは scattering amplitude) に対応します。そのため、このような変調構造を「振幅変調」 (amplitude modulation) と呼ぶことがあります。
振幅変調は散乱能の変化ですが、もう一つの重要な要素は「位相」です。位相が変調するとは、穴の大きさ(散乱能)は変わらないが、穴の位置が変化するということです。このような変調を「位相変調」 (phase modulation)といいます。以下の例は、格子パターン中の穴の大きさは全て等しいが、\(\bf{b}\) 軸の長さ (つまり位相) が6.28倍で変調している例です。
格子パターン (実空間) (位相変調 \(\bf{b’} = 6.28\bf{b}\))

回折パターン (逆空間)

振幅変調の例と同様に、基本スポットの周りに変調に由来する弱いスポットが出現していますが、強度分布 (特に透過スポット付近の様子) が異なっていることがわかります。
なお、非整数倍に変調した構造を厳密に取り扱う場合は、高次元の空間群で結晶構造を記述する必要があるのですが、その説明をするには私の能力が不足していますのでここでは割愛させていただきます。