対称性と対称操作/要素
対称性 (symmetry) とは、ある変換を施す前後で物体の状態が全く変わらない (invariant)、という性質のことです。そのような変換を対称操作 (symmetry operation) といいます。前ページの公園の例では、並進操作 (平行移動) という対称操作を施しても、公園の状態は全く変化しませんでした。別の言い方をすると、公園は並進要素という対称要素 (symmetry element) を有する物体であるということです。用語の使い方に混乱してきましたね。以下に、対称操作と対称要素の概念を詳しく説明します。
対称操作の分類と性質
対称操作とは、空間中におかれた物体を不変に保つような操作のことです。細かい数学的な意味づけや表現はすこし後回しにして、ここではざっくりと様々な対称操作の概要を説明します。まず対称操作には大きく分けて「並進を伴わない操作」と「並進を伴う操作」の2種類があります。
並進を伴わない操作
並進を伴わない操作は、何回か繰り返すと必ず元の場所に戻ってきます。言い換えると、空間中に不動となる点が必ず存在します。この種の操作を組み合わせると「点群」というものが得られるのですが、群については別の章で詳しく解説します。
| 恒等 (Identity) | 何もしない(動かさない) |
| 対称心 (Inversion) | 空間中のある点を原点として、x, y, z座標をすべて逆符号に変換 |
| 鏡映 (Reflection) | 空間中のある面に対して鏡で映すように変換 |
| 回転 (Rotation) | 空間中のある直線を軸として回転 |
| 回反 (Rotoinversion) | 回転操作に引き続き、回転軸上のある点を原点として対称心操作 |
恒等操作
「何もしない」という操作です。こんなの何の意味があるんだと思うかもしれませんが、この操作を認めることで群としての構造を満たすようになります。
対称心操作
この操作は、空間中のある点を原点と考え、その周りの物体のx, y, z座標をすべて逆符号に反転させる操作です。右手が左手に変換されます。
二回繰り返すともとの場所に戻ってきます。

鏡映操作
この操作は、空間中のある面に対して周りの物体を鏡のように映す操作です。この操作も右手が左手に変換されます。
二回繰り返すともとの場所に戻ってきます。

回転操作
空間中のある直線を回転軸として、その軸の周りの物体を回転する操作です。回転角度は一般的にはどんな値でも構いませんが、結晶を対象とした場合 (並進を含むような図形の場合) 回転角度は 60°, 90°, 120°, 180°, 240°, 270°, 360°のいずれかに限定されます。この操作では右手は右手のまま保存されます。
回転角度をn°とした場合、360/n 回この操作を繰り返すと元の場所に戻ります。回転角度が360°の時は「何もしない」わけですから、恒等操作と同一とみなすことができます。

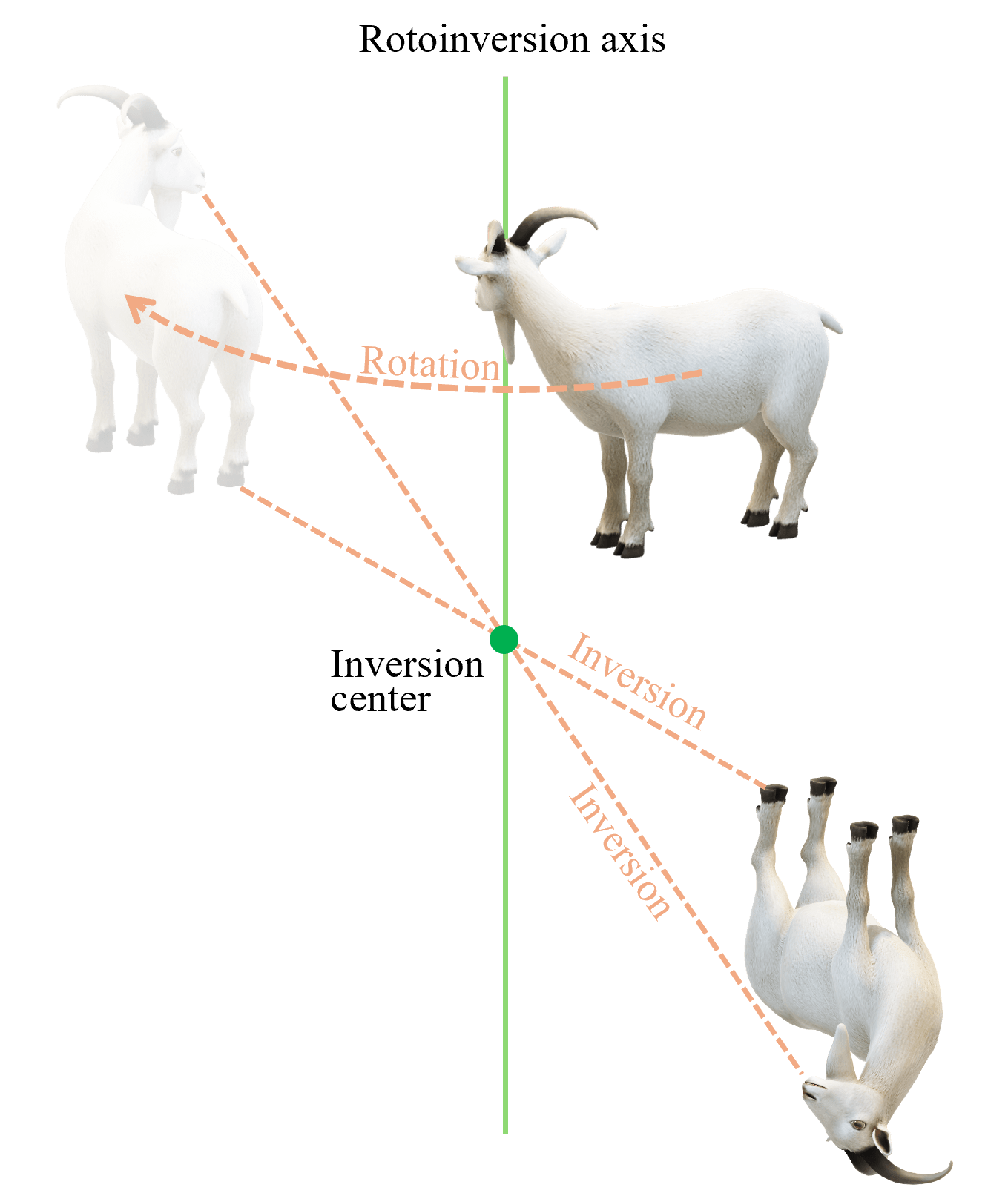
回反操作
回反操作とは一旦回転操作を施したあと、引き続き回転軸上のある点を原点として対称心操作を行うというものです。「回して反転」と覚えておくのがよいでしょう。この操作はイメージするのが難しく、初学者の方が最も躓きやすい操作かもしれません。なぜ、「引き続き」なのか?ふたつに分けたらいいではないか?と思われるでしょうが、この一連の操作をひとつの独立した操作と認めて(名付けて)おくと、いろいろと議論が簡単になるのです。
この操作では右手が左手に変換されます。また、回転操作の説明と同様の理由に、結晶を対象とした場合回転角度は 60°, 90°, 120°, 180°, 240°, 270°, 360° のいずれかに限定されます。回転角度をn°とした場合、360/n が偶数であれば360/n 回この操作を繰り返すと元の場所に戻ります。360/n が奇数であれば、720/n 回繰り返すと元の場所に戻ります。回転角度が360°の時は単なる対称心操作とみなすことができます。回転角度が180°の時は回反軸を法線とする鏡映操作とみなすことができます。
並進を伴う操作
並進を伴う操作は、何回か繰り返すともとの場所から離れていきます。この種の操作によって、空間中に不動となる点は存在しません。結晶は必ずこの種の操作を有していますし、この種の操作を含めば必ず結晶ということになります。並進を伴わない/伴う操作の集合は空間群を構成します。
| 格子並進 (Translation) | 単純な平行移動 |
| らせん (Screw) | 回転操作に引き続き、回転軸に沿って平行移動 |
| 映進 (Glide) | 鏡映操作に引き続き、鏡映面に沿って平行移動 |
格子並進
ある方向にある距離だけ、向きを変えずに平行移動する操作です。右手は右手のまま保存されます。

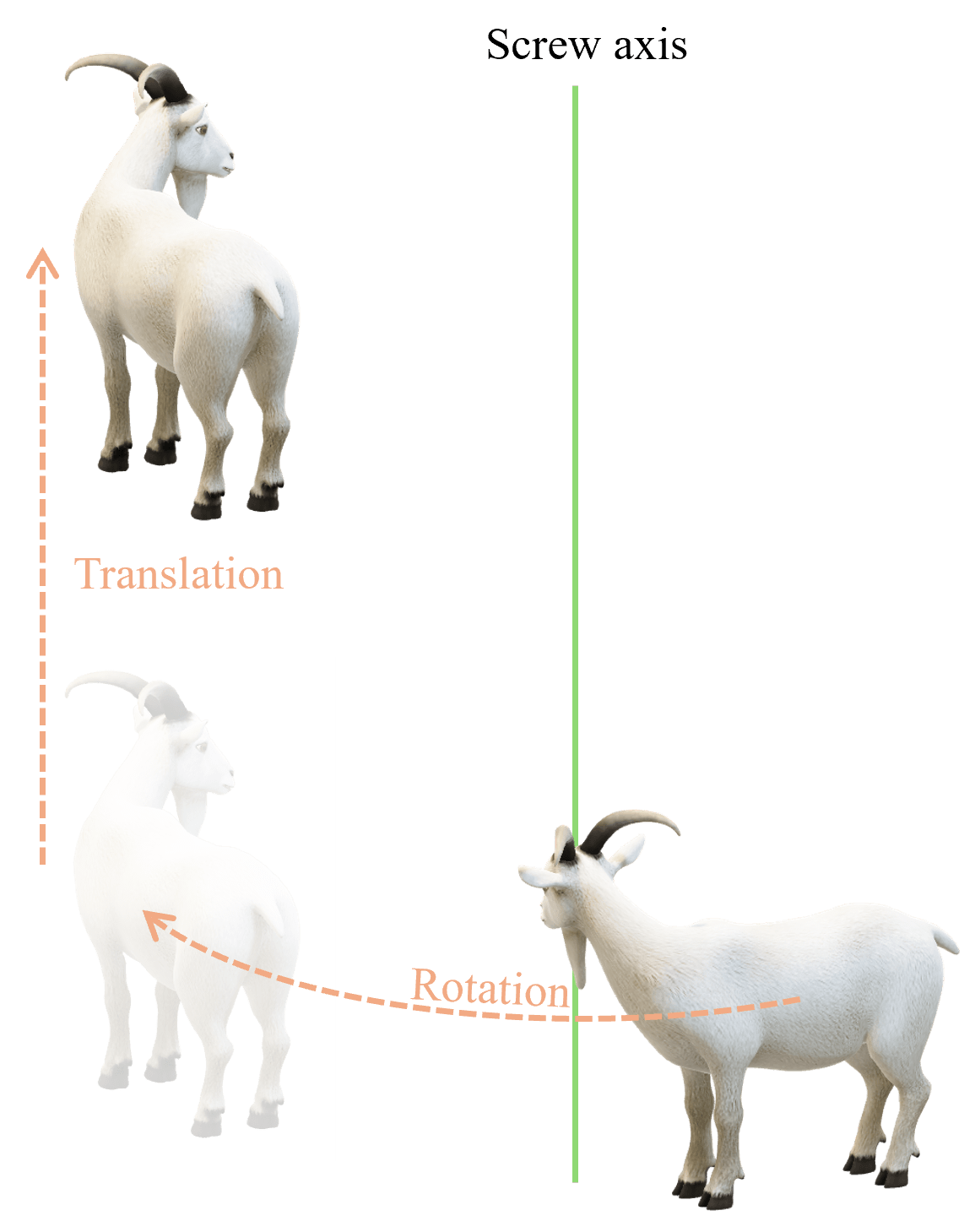
らせん
この操作は、回転操作を施したあと、引き続き回転軸に沿って並進操作を行うというものです。らせん階段をイメージするのが分かりやすいですね。右手は右手のまま保存されます。単なる2つの操作の組み合わせと思われるでしょうが、回反操作と同様、これも分類しておくと何かと便利なのです。
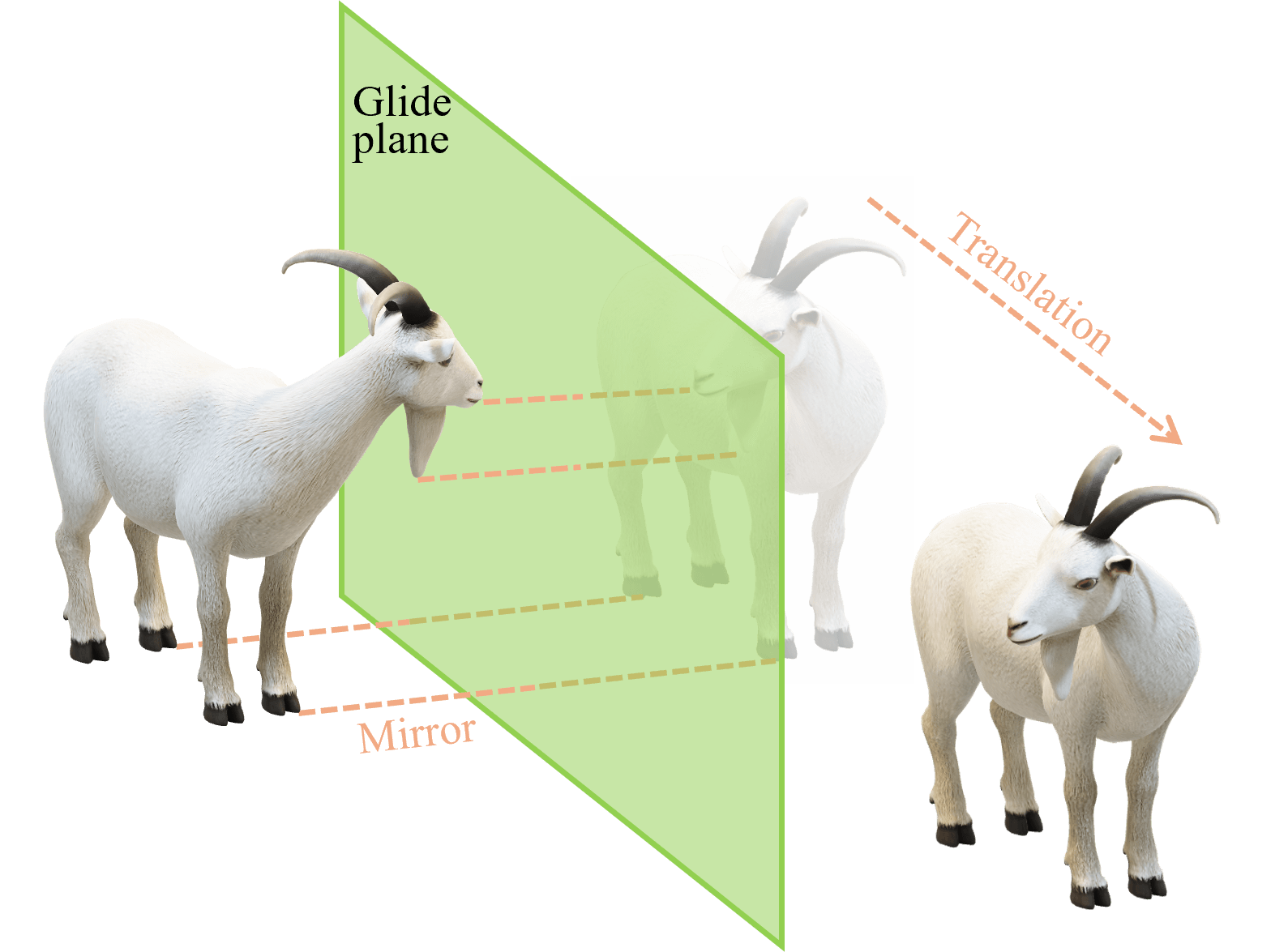
映進
鏡映操作を施したあと、引き続きその面と平行な方向に並進操作を行うというものです。右手は左手に変換されます。2つの操作の連続ですが、独立した操作として数えます。「映って進む」と覚えるのが良いでしょう。
まとめ
ここまでで紹介してきた操作は、何らかの対象を回したり動かしたりするという作業のことです。そして、その対象にその操作を施しても状態が不変であれば、「対称操作」であるということです。すべての対称操作は、体積や形状の変化を伴わない線形的な変換であり、これをユークリッド変換といいます(詳しくは別ページ)。
並進を伴わない対称操作は、恒等・対称心・鏡映・回転・回反の5種類あります。ただし、恒等操作は360°回転操作と同一であり、対称心操作と鏡映操作は回反操作の特別な場合だということを知っておくと、これから説明する対称要素の表記についての理解がより深まるでしょう。一方、並進を伴う対称操作は、格子並進・らせん・映進の3種類です。
この節で説明した対称操作が、3次元空間で可能な対称操作の全てです。意外と少ないと思われるかもしれませんが、世の中こんなものなのです。
対称要素
例えばこの世のすべての物体は恒等操作という対称操作に対して不変ですし、正四面体は120回転操作、240°回転操作、鏡映操作などに対して不変です。ただ、対称操作はあくまで操作 (回したり動かしたりという作業) であって、対象物が有する性質あるいは要素ではありません。それではなんらかの対称操作を許してくれるような、物体の有する性質を何と呼べばいいでしょうか?これがずばり「対称要素」という概念です。
対称要素とは、対称操作が行われる位置に存在し、その操作の性質 (鏡映、回転など) を有している、仮想的な点・線・面などのことです。対称操作の説明図では、緑色の点、線、面として表現しているものです。当然ながらそれらは実在しない仮想的な概念ですが、なぜこの考え方を導入する必要があるのでしょう?簡単な例で説明します。
次のような、90°回転操作によって不変に保たれるような図形があったとします。90°回転操作が許されるなら、当然180°, 270°, 360°回転操作も許されるはずです。つまりこれらの4つの操作を全てを許すような状態が必ず実現されます。でも、この図形の対称性を説明する際にわざわざ 「90°, 180°, 270°, 360°回転操作によって不変に保たれる図形」 と説明するのは面倒ですよね。
ここで対称要素の登場です。この図形は仮想的な緑の直線で表した “\(4\)” という対称要素を有していると考えるのです。”\(4\)” は4つの操作 (90°, 180°, 270°, 360°回転操作) を含んでおり、この要素(直線)の周りでどの4つの操作を施しても図形は不変に保たれます。対称要素の表現を導入すれば、この図形の対称性は 「\(4\) を有する」 とたった一言で表現できるというわけです。
「対称操作」は物体を不変に保つ操作であり、「対称要素」は物体が有する性質です。混同しやすい概念ですが、きちんと使い分けられるとカッコいいですね。

なお、対称要素は 「対称操作の行われる位置に存在する点・線・面などのことである」と説明しましたが、例外があります。まず恒等操作に対応する対称要素は、点・線・面のような一定の幾何学的形状を持ちません (あえて言えば、空間の全てに存在しています)。もうひとつ、並進要素は結晶が必ず有する対称要素ですが、この要素は特定の位置に存在しているわけではなく、方向と長さだけで定義されるベクトルの性質を持った対称要素であり、単位格子の概念に他なりません。
対称要素の表記
以下に、国際結晶学会が策定している国際標準の対称要素の表記を紹介します。結晶 (並進対称性を有する物体) に現れる対称要素のみに限定しています。対称要素は数字やアルファベットで表記されますが、数字は斜体にせず、アルファベットは斜体にするというルールがあります。なお、対称操作の表記については後述するザイツ記号を用いるのが一般的です。ザイツ記号は以下の対称要素表記がベースとなっているので、まずはこちらをきちんと押さえておきましょう。
並進を伴わない対称要素
| 名称 | 表記 | 説明 |
|---|---|---|
| 恒等 | \(1\) | 360°回転と同義 |
| 対称心 | \(\bar{1}\ (=i)\) | 360°回反と同義 \(i\)と表現することもある |
| 鏡映 | \(m\ (=\bar{2})\) | 180°回反と同義 |
| 回転 | \(2\), \(3\), \(4\), \(6\) | 回転の次数 (360°/回転角度) で表現 |
| 回反 | \(\bar{1}\ (=i)\), \(\bar{2}\ (=m)\), \(\bar{3}\), \(\bar{4}\), \(\bar{6}\) | 回転の次数 (360°/回転角度) で表現 |
回転要素や回反要素は、回転角度ではなく、「360°÷ 回転角度」 の数値で表現します。これを回転あるいは回反の次数といいます。
回転要素は回転の次数そのままの数字です。発音は、例えば\(4\)の場合、「よん」、「4回回転1」、「four」などです。一方、回反要素は次数の上にバーがついた記号で表現します。発音は、例えば\(\bar{4}\) の場合、「マイナスよん」、「4回回反」、「bar four」などです。
並進を伴う対称要素
| 名称 | 表記 | 説明 |
|---|---|---|
| 格子 並進 | \(P\) \(A, B, C\) \(I\) \(F\) \(R\) | 単純格子 底心格子 体心格子 面心格子 菱面格子 |
| らせん | \(2_1\) \(3_1\), \(3_2\) \(4_1\), \(4_2\), \(4_3\) \(6_1\), \(6_2\), \(6_3\), \(6_4\), \(6_5\) | ひとつめの数字は回転の次数、ふたつめの数字は並進割合 (並進量 = 軸方向の周期 × ふたつめの数字 / ひとつめの数字) |
| 映進 | \(a\), \(b\), \(c\) \(n\) \(e\) \(d\) | 軸映進面 対角映進面 二軸映進面 ダイヤモンド映進面 |
並進を伴う対称要素は結晶にのみ存在します。普通の並進要素はもちろん、らせん要素や映進要素も、結晶の中だけに存在しうる対称要素です。
並進要素は大文字のアルファベットで表現します。\(P, A, B, C, I, F, R\) という七つの記号があり、単位格子の種類を表します。次のページ 「1.3. 格子定数・結晶系・ブラベー格子」でこれらの記号の意味を説明します。
らせん要素は、二つの数字で表現されます。ひとつめの数字(通常サイズ)は回転の次数に対応し、ふたつめの数字(下付き)は並進量に対応します。らせん軸の方向は、かならず結晶中の並進ベクトル(格子点と格子点を結ぶベクトル)の方向と一致します2。らせん要素の並進量は、らせん軸に沿った並進の最小周期に対する「ふたつめ数字 / ひとつめの数字」と定義されます。たとえば、\(4_3\) という対称要素を有する結晶は、「90°回転し、軸に沿って軸の周期の3/4だけ進む」という操作によって不変に保たれます。発音は、例えば \(4_3\) の場合、「よんさん(らせん)」、「four sub three (screw)」 などが普通です。個々のらせん要素がどのような性質であるか、改めて「3.1. 対称要素の詳細」で説明します。
映進要素は、小文字のアルファベットで表現します。たくさんの記号があって分かりにくいですね。これらについても、改めて「3.1. 対称要素の詳細」で説明します。