原点選択の方針
空間群を使って結晶構造を組み立てるとき、原点選択 (Origin choice) という概念があります。単位格子の原点座標の選び方が2つある一部の空間群において、注意しなければいけない概念です。
単位格子とは独立な格子並進ベクトルを三辺とするような格子のことです。ベクトルの原点座標 (始点) をどこと考えようが、それによって結晶の性質は何ら変化しません。とはいえ単位格子の原点の選び方に個人差があると、無用な混乱が生じてしまいます。対称操作として格子並進しかないケース(=空間群 \(P1\) )であれば好き勝手に選ぶしかありませんが、残りの229個の空間群は他の対称操作(回転・回反・らせん・映進)も有しており、それらは空間中に離散的に存在しています。このような(並進以外の)対称操作の空間配置を単位格子の原点位置と結び付けて考えた方がきっと混乱が少なるだろう、と昔の偉大な結晶学者たちは考えました。現在普及している国際標準 (=IUCr [国際結晶学会]策定)の単位格子原点の選び方は、以下の三つの方針でまとめることができます。
- 方針1: \(\bar{1}\) (対称心)を有する空間群の場合は \(\bar{1}\) の位置を原点として選ぶ。
- 方針2: その空間群の最高のサイトシンメトリーの位置を原点として選ぶ。ただし、\(1\) より高いサイトシンメトリーが無い場合は、らせん軸か、映進面か、あるいはそれらの交線や交点上を原点として選ぶ。
- 方針3 (特例): 空間群 \(P2_12_12_1\) (直方晶系) およびその超群である空間群\(I2_12_12_1\) (直方晶系)と \(P2_13\) , \(I2_13\) , \(F4_132\) , \(P4_332\) , \(P4_132\) , \(I4_132\) (立方晶系) はすべて対称心を有しないが、特例として方針2には従わず、三本の交わらない \(2_1\) らせん軸に(分率座標空間で)等距離で取り囲まれるような点を原点とする。
サイトシンメトリーとは、結晶中のある点から周りを見渡した時、どのような点対称性があるかを示しています (詳しくは「サイトシンメトリーとワイコフ位置」ページをご覧ください)。ほとんどの空間群 (230種の空間群のうち206種) では上記三つの方針によって原点をただ一つに決めることができます。ただ、方針1が示す位置と方針2が示す位置が異なってしまうような空間群もあります。そうです、これが原点を決める際に複数の選択肢が生じる状況です。230種のうち24種の空間群については、方針1に従うか、あるいは方針2に従うか、使用者に判断がゆだねられます。
例
たとえば空間群 \(Pmmn\) において、もっとも高いサイトシンメトリーは \(mm2\) です。この位置には2回回転操作が存在し、さらにミラー2枚が交差しています。これを原点とするのが 「原点選択 1」 です。また、\(mm2\) の位置から \((\frac{1}{4} \frac{1}{4} 0)\) だけずれた位置に \(\bar{1}\) (対称心)もあります。この位置を原点とするのが 「原点選択 2」 です。
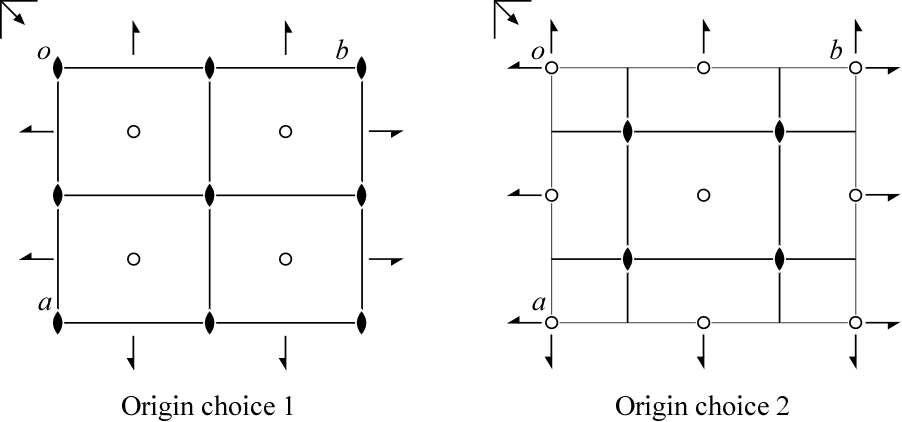
上に空間群\(Pmmn\)の原点選択1 (Origin choice 1)と原点選択2 (Origin choice 2)の対称操作の配置を示しました。下が \(a\) 軸方向、右が \(b\) 軸方向、紙面垂直手前が \(c\) 軸方向です。左上の\(“o”\)の位置が原点となります。左右の図は、\((\frac{1}{4} \frac{1}{4} 0)\)だけずれた関係になっているのが分かりますね。
このような二つの原点セッティングを考慮しなければいけない空間群は、直方晶系・正方晶系・立方晶系のいずれかに属しており、全部で24個あります。以下に全てを羅列します。文献に書かれている結晶の空間群が下記のいずれかに該当する場合は、原点選択が1か2のどちらであるかをきちんと見極めないと間違った解釈につながるかもしれませんのでお気を付けください。
| 直方晶系 (Orthorhombic) | 点群 \(mmm\) | \(Pnnn, Pban, Pmmm, Ccce, Aeaa, Fddd\) |
| 正方晶系 (Tetragonal) | 点群 \(4/m\) | \(P4/n, P4_2/n, I4_1/a\) |
| 点群 \(4/mmm\) | \(P4/nbm, P4/nmm, P4/ncc, P4_2/nbc, P4_2/nnm\) \(P4_2/nmc, P4_2/ncm, I4_1/amd, I4_1/acd\) | |
| 立方晶系 (Cubic) | 点群 \(m\bar{3}\) | \(Pn\bar{3}, Fd\bar{3}\) |
| 点群 \(m\bar{3}m\) | \(Pn\bar{3}n, Pn\bar{3}m, Fd\bar{3}m, Fd\bar{3}c\) |
繰り返しになりますが、原点選択が1でも2でも、結晶の性質が変わるわけではありません。どちらで表現しても構いませんが、もし相転移(空間群変化)を伴うような現象を議論する場合は比較対象となる空間群の原点と整合性のある原点選択をするのが良いでしょう。