5.0. 概要
回折シミュレータは、メインウィンドウで選択した結晶に対して、単結晶X線回折、電子回折、中性子回折のシミュレーションを行います。
X線が線源の場合は平行単色ビームに加えてプレセッションカメラやバックラウエカメラの回折光学系に対応します。電子線が線源の場合は、制限視野回折、プレセッション電子回折、収束電子回折の回折光学系に対応します。中性子が線源の場合は平行単色ビームの回折光学系にのみ対応します。
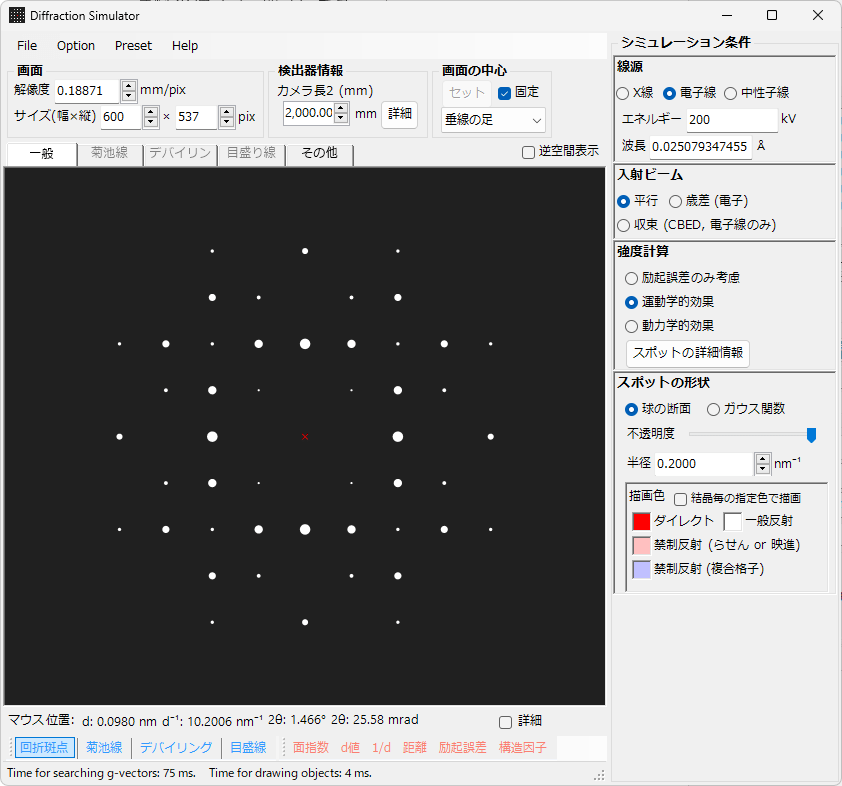
5.1. メイン描画エリア
画面の中央に表示されているエリアに、回折パターンをシミュレーションします。標準ではダイレクトスポットは赤い✕印で、検出器からおろした垂線の足は緑の✕印で表示されます。また、検出器のピクセル数や解像度を設定している場合は検出器範囲が緑の枠で表示されます。
メイン描画エリアでは、以下のようなマウス操作に対応します。
- Left drag: 回転
- Center drag: 平行移動
- Right drag: 拡大
- Right click: 縮小
- Left double click: 選択したスポットの詳細情報を表示
マウス位置情報

メイン描画エリア内にマウスポインタがある場合、その位置に相当する情報を表示します。「詳細」 をチェックすると表示領域が拡張し、より細かい情報が表示されます。
5.2. ファイルメニュー
5.2.1. File
Save / Save detector area
表示されている画像を保存します。後者は検出器のピクセル数や解像度を設定している場合に表示されます。
Save / Save detector area
表示されている画像を保存します。後者は検出器のピクセル数や解像度を設定している場合に表示されます。
5.2.2. Preset

プリセットされている典型的な入射線源が表示されます。選択すると入射線源が変更されます。
5.3. 画面 / 検出器情報/ 画面の中心

5.3.1. 画面
解像度
1 ピクセルあたりの長さ(mm)を設定します。この値は単なるスケールの問題なので、実際の値でなくてもかまいません。マウスによる拡大縮小で変更されるパラメータです。
サイズ
描画エリアの幅と高さをピクセル数で指定します。お使いのディスプレイの解像度によっては自由な値を設定できない場合があります。
5.3.2. 検出器情報
検出器の幾何学的な位置関係を表示/設定します。
カメラ長 2
試料から検出器までの距離を表示/設定します。
詳細
検出器の幾何学的な位置や解像度などの関する詳細設定画面が起動します。詳しくは 5.8. 検出器詳細情報あるいはA1. 座標系の定義をご覧ください。
5.3.3. 画面の中心
画面の中心を設定します。以下の三つの選択肢をコンボボックスから選択します。
- 垂線の足:試料から検出器におろした垂線の足を画面の中心に設定します。
- ダイレクトスポット:入射線と検出器が交わる点を画面の中心に設定します。
- 検出器の中心:検出器範囲の中心を画面の中心に設定します。検出器情報を正しく設定している必要があります。
セット
このボタンを押すと、画面の中心がコンボボックスで選択された位置と一致します。
固定
これがチェックされていると、常に画面の中心は画面の中心がコンボボックスで選択された位置と一致します。
5.4. タブメニュー
5.4.1. 一般
スポット、文字などの色の設定を行います。
背景/文字/垂線の足
それぞれの色を指定します。
文字サイズ
文字のサイズをスライドバーで設定します。
5.4.2. 菊池線
菊池線に関する設定を行います。ツールバーで 「菊池線」 を選択しているときにアクティブになります。
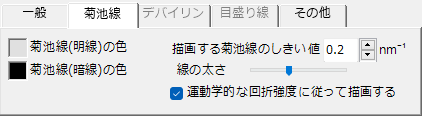
菊池線 (明線/暗線)の色
描画する菊池線の色を指定します。背景と全く同じ色にならないようにご注意ください。
描画する菊池線のしきい値
この値より大きなd値をもつ菊池線を計算対象とします。
線の太さ
菊池線の太さを指定します。
運動学的な回折強度に従って描画
菊池線を描画する際、運動学的回折強度に従って
5.4.3. デバイリング
ツールバーで 「デバイリング」 を選択しているときにアクティブになります。
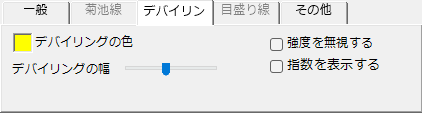
デバイリングの色/デバイリングの幅
描画するデバイリングの色や線幅を指定します。
強度を無視する
構造因子を考慮せず、全て同じ色で描画します。
指数を表示
デバイリングの近くに結晶面指数を表示します。
5.4.4. 目盛り線
ツールバーで「目盛線」を選択しているときにアクティブになります。
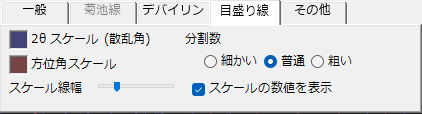
2θ スケール / 方位角スケール
前者は散乱角方向、後者は方位角方向を意味しています。それぞれ目盛線の色を変更できます。
スケール線幅
目盛線の太さをスケールバーで設定します。
分割数
目盛線の目盛間隔を設定します。
スケールの数値を表示
目盛線にラベルを表示するかどうかを選択します。
5.4.5. その他
マウスで回転するときの感度
マウス操作をする際のマウス感度を設定します。
5.5. シミュレーション条件
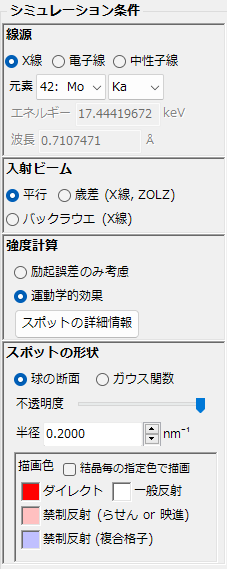
回折スポットの計算、表示などに関するシミュレーション条件の設定を行います。選択されている入射線源の種類や入射ビームの種類によって、表示される項目が変化します。
5.5.1. 線源
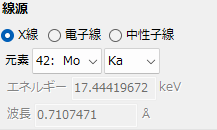
入射する線源の種類を選択します。
- X線: 特性X線の場合は、ターゲットの原子とラインを選んでください。任意のエネルギー/波長を設定したい場合は、コンボボックスから「0: Custom」 を選択してください。
- 電子線: 任意のエネルギー/波長を設定してください。
- 中性子線: 任意のエネルギー/波長を設定してください。
5.5.2. 入射ビーム
X線の場合

線源にX線を選択すると、以下の選択肢が表示されます。
- 平行:細く絞ったX線を想定したシミュレーションを行います。
- 歳差:検出器と試料を同期的に歳差運動させた結果得られる回折パターン(いわゆるプリセッションカメラ) のシミュレーションを行います。
- バックラウエ:入射X線が 0-50keV の範囲でフラットな強度を持つ白色X線を想定したバックラウエの回折パターンをシミュレーションします。
電子線の場合

線源に電子線を選択すると、以下の選択肢が表示されます。
- 平行:平行で細く絞った電子線を想定したシミュレーションを行います。いわゆる SAED (selected area electron diffraction) のことです。
- 歳差:入射ビームを歳差運動させて得られる回折パターンをシミュレーションします。いわゆるPED (precession electron diffraction) です。このモードを選択すると、「強度計算」は自動的に「動力学的効果」に設定されます。
- 収束:大きな半頂角で収束させて得られる回折ディスクをシミュレーションします。いわゆる CBED (convergent beam electron diffraction)です。このモードを選択すると、「強度計算」は自動的に「動力学的効果」に設定され、後述する専用の設定画面が現れます。
中性子線の場合

線源に中性子線を選択した場合は、「平行」のみが表示されます。
- 平行:細く絞った中性子線を想定したシミュレーションを行います。
5.5.3. 強度計算
回折スポットの強度の計算方法を選択します。

励起誤差のみ考慮
励起誤差 (逆空間におけるエワルド球面と逆格子点との距離)を元に強度を計算します。励起誤差が小さいほど強度は高くなり、その最大値は後述する 「半径」 の値となります。励起誤差が大きくなると強度は小さくなり、「半径」 を超えるとゼロになります。
運動学的効果
励起誤差に加えて、結晶構造因子も考慮して回折強度を計算します。
動力学効果
動力学的回折理論 (ブロッホ波法)を使って、回折強度を計算します。線源として電子線を選択している場合のみ選択可能です。
スポットの詳細
回折スポットの詳細情報を表示します。5.10. スポットの詳細 の項をご覧ください。
5.5.4. スポットの形状/色
回折スポットの表示の仕方を設定します。
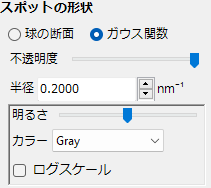
球の断面/ガウス関数
球の断面を選択した場合、逆格子点を中心にある半径をもったRの球体を仮定し、その球体とエワルド球との断面(すなわち円)を回折スポットとして表示します。円の面積が回折強度に対応します。
ガウス関数を選択した場合、逆格子点を中心にある標準偏差 (\(σ\)) とある積分強度 (\(I\)) をもった3次元ガウス関数1を仮定し、その3次元ガウス関数とエワルド球との断面に現れる2次元強度分布 (2次元ガウス関数) を回折スポットとして表示します。2次元ガウス関数の積分強度が、回折強度に対応します。
不透明度
描画する回折スポットの透明度を指定します。
半径
逆格子点の半径に相当する量を指定します。ここで指定した値 (以下 \(R\) とします) は、「スポット形状」および「強度計算」の選択肢によって、次のように回折スポットの表示方法に影響します。なお以下の説明では、ガウス関数の標準偏差を \(σ\) とし、後述する「明るさ」 値を \(B\) とします。
| スポットの形状 | 強度計算 | 回折スポットの表示方法 | ||
|---|---|---|---|---|
| 「ガウス関数 」 | 「励起誤差のみ考慮」 | \(R\) が標準偏差 \(\sigma\) であるような 3次元ガウス関数を仮定 | 3次元ガウス関数の積分強度は \(B\) | 3次元ガウス関数とエワルド球との断面に現れる強度分布(2次元ガウス関数)を回折スポットとして表示 |
| 「運動学的効果」 | 3次元ガウス関数の積分強度は \(B\) × [運動学的な相対回折強度] | |||
| 「動力学効果」 | \(R\) が標準偏差 \(\sigma\) であるような 2次元ガウス関数を仮定 | 2次元ガウス関数の積分強度は \(B\) × [動力学的な相対回折強度] | 左で定義される2次元ガウス関数を回折スポットとしてそのまま表示2 | |
| 「球の断面」 | 「励起誤差のみ考慮」 | \(R\) が半径である球体を仮定 | 左で定義される球体とエワルド球との断面を回折スポットとして表示 | |
| 「運動学的効果」 | \(R\) ×[運動学的な相対回折強度]1/3が半径である球体を仮定3 | |||
| 「動力学効果」 | 半径が \(R\) ×[動力学的な相対回折強度]1/2 である円を回折スポットとして表示 (円の面積は動力学的な相対回折強度に比例) | |||
明るさ (ガウス関数を選択した場合のみ)
上で述べた \(B\) の値です。スケールバーで調節します。
カラー (ガウス関数を選択した場合のみ)
Gray scale, Cold-warm color, Spectrum, Fire の中から選択します。
ログスケール (ガウス関数を選択した場合のみ)
チェックすると強度がLog scaleで表示されます。
描画色
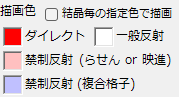
回折スポットの色を設定します。
禁制反射は、本来消滅側によって強度がゼロになる回折スポットですから、「励起誤差のみ考慮」で計算している場合のみ意味のある設定項目です。
5.5.5. ブロッホ波関連
ブロッホ波設定 ( 「電子線」 + 「動力学効果」 を選択した場合のみ)
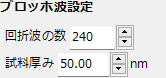
動力学的回折強度計算の際に取り入れるBloch 波の数を設定します。Bloch波法では、回折強度を計算するコストがこの数値の3乗に比例しますので、様子を見ながら徐々に増やしていってください。
試料厚み
試料の厚みを設定します。Bloch波法では試料厚みは計算速度に関係しません。
プリセッション設定 ( 「電子線」 + 「歳差」 を選択した場合のみ)

半頂角
歳差電子回折における入射電子の半頂角を設定します。
ステップ
歳差電子回折は、複数の方向からの平行ビーム電子回折を足し合わせることによってシミュレーションします。この方向の数を設定します。
5.6. ツールバー

5.6.1. 描画対象のオブジェクト
回折斑点
回折斑点の表示/非表示を切り替えます。
菊池線
菊池線の表示/非表示を切り替えます。
デバイリング
デバイリングの表示/非表示を切り替えます4。
目盛り線
目盛り線の表示/非表示を切り替えます。
5.6.2. 表示情報
面指数 / d値 / 1/d / 励起誤差 / 構造因子
スポットの近くに表示されるラベルの情報を選択します。
5.7. 逆空間表示
画面上部にある 「逆空間表示」 をチェックすると、メイン描画エリアの右にエワルド球面と逆格子点の関係を示す画面が表示されます。
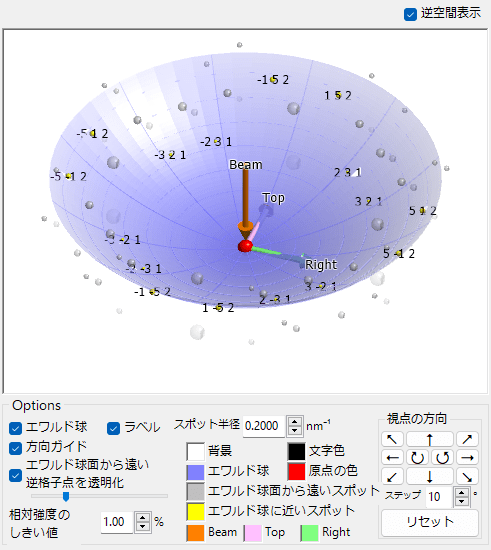
マウス操作
- 左ドラッグ: (結晶ではなく)視点の方向の回転
- 右ドラッグ (上下):拡大縮小
エワルド球
エワルド球の表示/非表示
方向ガイド
入射ビーム、画面上方向、画面右方向を示す矢印の表示/非表示
エワルド球面から遠い逆格子点を透明化
スライドバーで調節
相対強度の閾値
強度計算で「運動学的効果」あるいは「動力学効果」を選択している場合に、相対強度がしきい値を超える逆格子点のみを計算します。
スポット半径
逆格子点を表す球の半径を設定します。
色
描画色を設定します。
視点の方向
視点の方向を矢印ボタンで調節します。リセットを押すと初期状態に戻ります。
5.8. 検出器詳細情報
検出器に関する詳細な設定を行います。
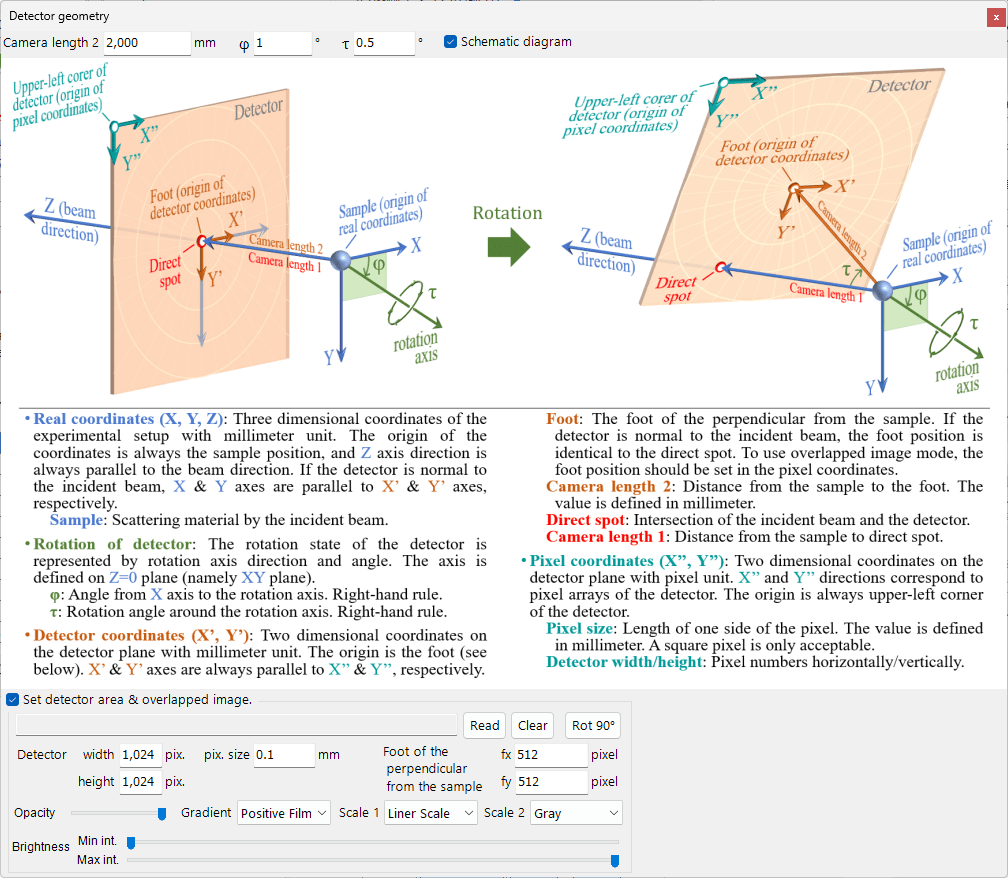
Schematic diagram
パラメータの意味を説明する模式図が表示されます。詳しくはA1. 座標系の定義を参照してください。
Set detector area & overlapped image
検出器のピクセル数やピクセルサイズを設定することで、シミュレーションした回折パターンに検出器画像を重ね合わせたり、検出器画像の枠線だけを表示することが出来ます。検出器の領域は緑色の矩形として表示されます。
画像を重ね合わせる場合は、Readボタンを押して画像を読み込みます。その後、ピクセルサイズや垂線の足を正しい値に設定してください。画像の透明度、色スケール、輝度なども調整することが出来ます。
検出器の枠線だけを表示したい場合は、画像を読み込まず、ピクセルサイズやピクセル数、垂線の足を設定してください。
5.9. CBED 設定
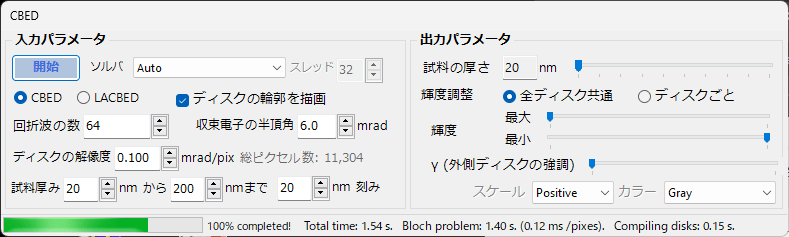
CBEDは大きなリソースを必要とする計算です。そのため、リアルタイムで計算は行いません。”Execute”ボタンを押して計算を実行します。
5.9.1. 入力パラメータ
CBEDの計算に必要な種々の入力パラメータを表示/設定します。
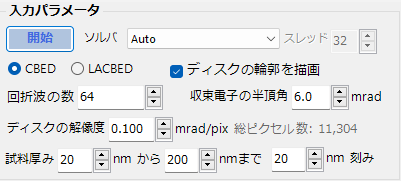
CBED/LACBED
通常の収束電子回折 (CBED)か、大角度収束電子回折 (large-angle CBED)かを選択します。前者は計算対象の回折ディスクを全て描画するのに対し、後者は g=0 の回折ディスクのみを描画します。
ソルバ
Bloch波法では固有値・固有ベクトルの計算に大きなリソースが消費されます。固有値問題を解くアルゴリズム(ソルバ)を以下から選択できます。
- Auto: 以下の三つから自動で高速のものを選択します。
- MKL:Intel社のライブラリMKL (https://software.intel.com/en-us/mkl) を使用します。
- Eigen: オープンソースライブラリEigen (https://gitlab.com/libeigen/eigen)を使用します。
- Managed: オープンソースライブラリMathnet (https://github.com/mathnet/)を使用します。
作者の経験によれば、Bloch波の数が小さい(< ~500)場合はEigenが、大きい場合(> ~500)はMKLが最も高速です。
回折波の数
何個のBloch波を計算に取り入れるかを指定します。計算量はBloch waveの数の3乗に比例しますので、大きな値を入れた場合は計算時間が長くなります。
収束電子の半頂角
電子線の収束角を指定します。
ディスクの輪郭を描画
CBEDのディスクの大きさを示すガイドをメイン描画エリアに表示します。半頂角を決定する際に参考にしてください。
ディスクの解像度
CBEDのディスクの解像度を指定します。ディスクはおよそ[半頂角]/[解像度]の二乗にπ/4を乗じたピクセルに分割されます。ピクセル数は計算量に単純比例しますので、小さな解像度にした場合は計算時間が長くなります。
試料厚み ## nm から ## nm まで ## nm 刻み
設定された複数の厚みに対してCBEDシミュレーションを行います。本ソフトではBloch波法による動力学的計算を行いますので、厚みが変化しても計算量はほとんど変化しません。
5.9.3. 出力パラメータ
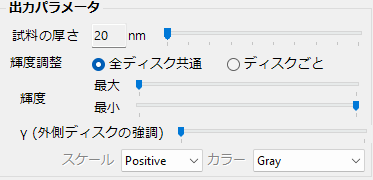
試料の厚さ
表示する試料厚みを指定します。
輝度調整
CBEDディスクはディスク間の輝度の差が非常に大きいことがあるため、全ディスク共通の輝度調整を行うか、ディスクごとに輝度調整を行うかを選択することができます。
輝度
スケールバーで輝度を調整して下さい。
γ (外側ディスクの強調)
散乱角の高いディスクの輝度を高くするパラメータです。
スケール/カラー
CBEDディスクの描画色を設定します。
5.10. 回折スポットの詳細
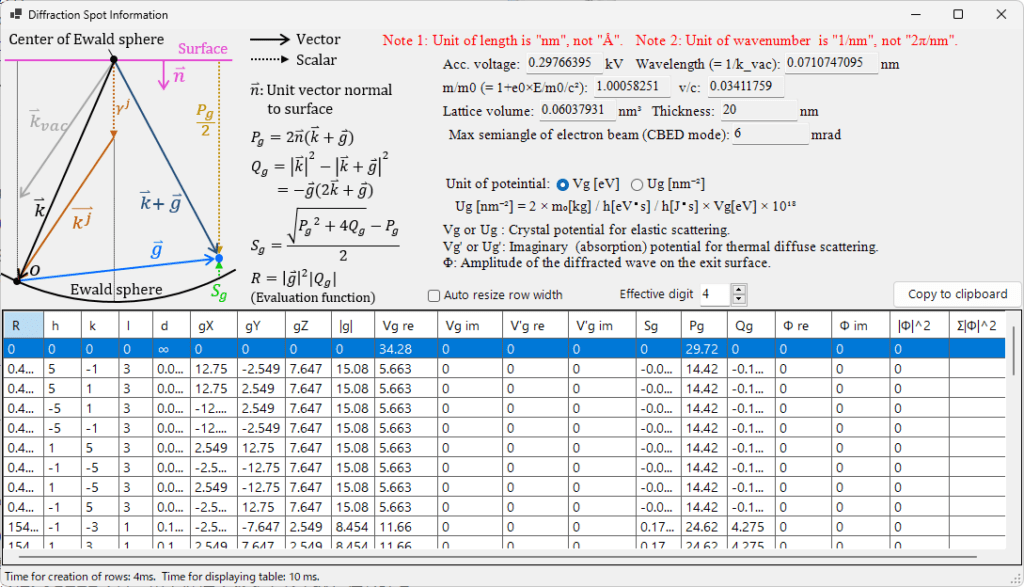
回折スポットの詳細情報を表示されます。記号の意味は、左上の模式図を参考にしてください。
Copy to clipboard
表の内容をクリップボードにコピーします。エクセルへの貼り付けが可能なタブ区切り形式です。
シミュレーション例
- 原点を中心とする、標準偏差が \(\sigma\) の3次元ガウス関数は、$$
f(x,y,z)= \frac{I}{\sigma^3(2\pi)^{3/2}}\exp\left( -\frac{x^2+y^2+z^2}{2\sigma^2} \right)
$$のような書くことが出来ます。この関数を3次元全空間で積分した値は \(I\) です。この3次元ガウス関数を \(z=Z\) で切り取った断面は、$$
f(x,y,z=Z)= \frac{I}{\sigma^3(2\pi)^{3/2}}\exp\left( -\frac{Z^2}{2\sigma^2} \right)\exp\left( -\frac{x^2+y^2}{2\sigma^2} \right)
$$という形になります。これを \(x,y\) で無限まで積分して得られる値は、\( \displaystyle \frac{I}{\sigma\sqrt{2\pi}}\exp\left( -\frac{Z^2}{2\sigma^2} \right)\) となります。 ↩︎ - 当然、動力学計算の際に励起誤差の影響は考慮されています。 ↩︎
- 球体の体積を運動学的な相対回折強度に比例させるために、1/3乗しています。 ↩︎
- Debye ringsとは、本来試料が多結晶体であるときに現れる回折スポットの集合体です。当然ながらデバイリングのシミュレーションでは、単結晶としての向きは考慮せず、多数のランダムな方位の結晶からの回折パターンを計算します。 ↩︎