9.0. 概要
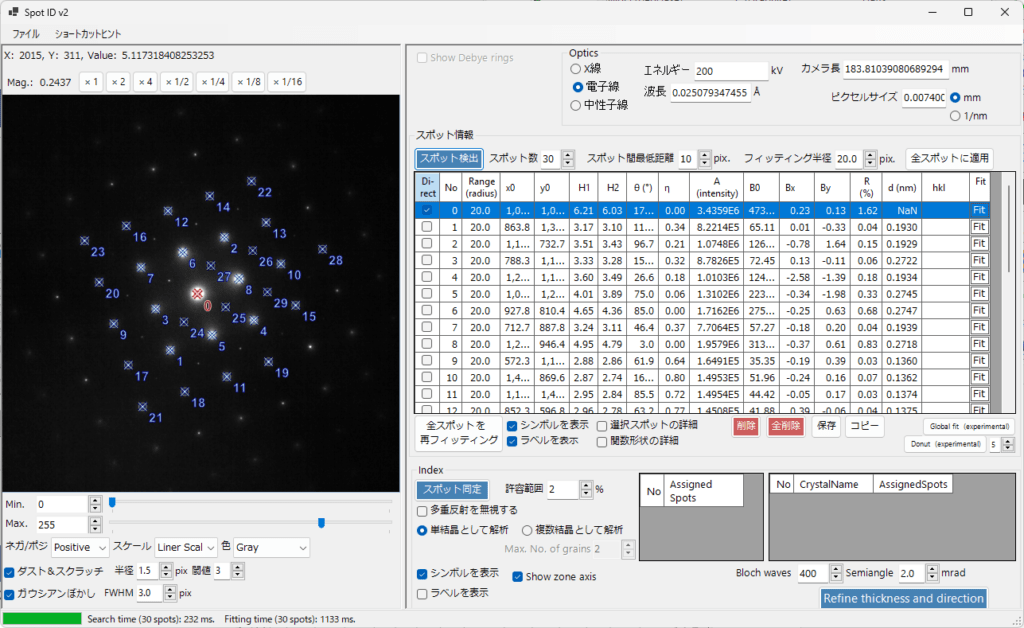
回折パターンが記録された画像中からスポットを検出し、指数付けを行います。Digital MicrographなどのTEM用カメラで撮影したファイルを直接読み込むことが出来、条件が整えば試料厚みの推定も行うことが出来ます。
9.1. 画像表示エリア
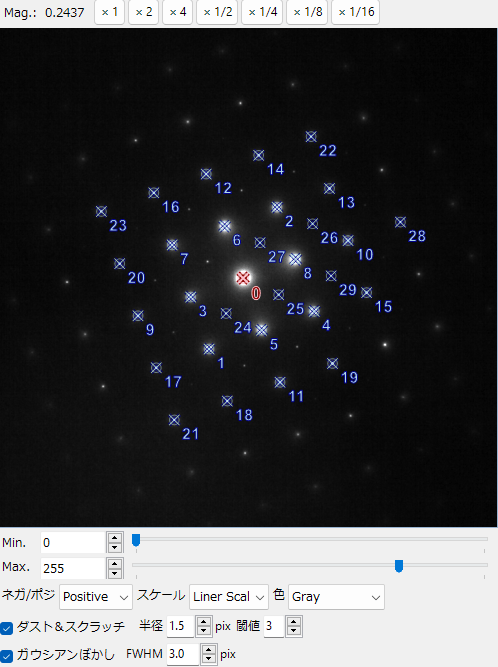
画像を表示するエリアです。画像ファイルをドラッグドロップするか、Fileメニューから読み込んでください。jpg, tif, dm3, dm4形式に対応しています。
マウス操作
右クリックで縮小、右ドラッグで拡大できます。さらに以下のようなマウス操作を受け付けます。
- 左シングルクリック: スポット選択
- 左ダブルクリック: スポット追加
- Ctrl+左ダブルクリック: ダイレクトスポット追加
- Ctrl+右シングルクリック:スポット削除
倍率ボタン (×1, ×2, …)
指定した倍率に画像を拡大/縮小します。
Min/Max
画像の最大輝度、最低輝度を設定します。トラックバーで調整することもできます。
ネガ/ポジ
Positiveで表示するかNegativeで表示するかを選択します。
スケール
LinearスケールかLogスケールかを選択します。
色
Gray, Cold-Warm, Spectrum, Fire のいずれかを選択します。
ダスト&スクラッチ
画像中の1ピクセルないし数ピクセルから成る輝点を除去します。輝点の検出範囲をピクセル単位で指定し、検出の閾値を標準偏差の倍数で指定してください。
Gaussian blur
画像に対して、ガウス関数によるフィルター(ぼかし)をかけます。ぼかしの範囲はピクセル単位で指定します。
9.2. Optics

入射線源、エネルギー/波長、カメラ長、検出器のピクセルサイズを入力します。*.dm3あるいは*.dm4ファイルを読み込んだ場合は、ファイル内の情報を使って自動的にセットされます。
9.3. スポット情報
スポットを検出・フィッティングする条件を設定し、その結果が中央のテーブルに表示されます。
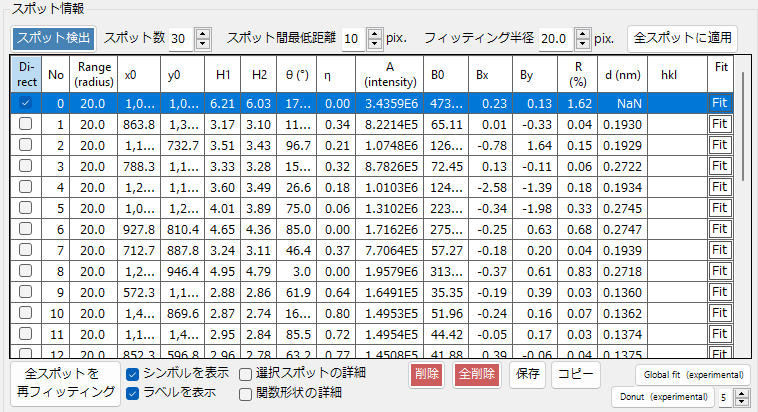
上部
スポット検出
画像を読み込んだ後「スポット検出」 ボタンを押すと、画像中の回折スポットを自動で検出し、そのスポットを2次元Pseudo Voigt関数1でフィッティングします。フィッティングの結果は、テーブルに表示されます。
スポット数
検出するスポットの最大数を設定します。
スポット間最低距離
検出するスポット間の最低距離を設定します。
フィッティング半径
検出されたスポットを2次元Pseudo Voigt関数でフィッティングする際の範囲を、ピクセル単位の半径で指定します。
全スポットに適用
テーブル中のスポットのフィッティング範囲を再セットします。
中央部
中央部にはフィッティング結果がテーブルとして表示されます。セル内の内容はダブルクリックすることで編集可能となります。
各行の一番左にある「Direct」をチェックすると、チェックしたスポットがダイレクトスポットとして扱われます。各行の一番右にある「Fit」ボタンを押すと、そのスポットに対してのみフィッティングが再実行されます。
下部
全スポットを再フィッティング
テーブル中の全てのスポットに対して、再度フィッティングを行います。
シンボルを表示/ラベルを表示
検出されたスポットのラベルおよびシンボルを、画像にオーバーラップして表示するかどうかを選択します。
選択スポットの詳細
チェックすると、以下のような別ウィンドウが表示されます。
このウィンドウでは左側に選択されているスポットの拡大が表示され、右側には4つの方向のプロファイルが表示されます。青い線が画像のデータであり、赤い線がフィッティング結果に対応します。
関数形状の詳細
フィッティング関数が表示されます。
削除/全削除
選択しているスポット、あるいはテーブル中の全てのスポットを削除します。
保存/コピー
テーブルの情報をエクセル形式で保存あるいはクリップボードにコピーします。
9.4. Index
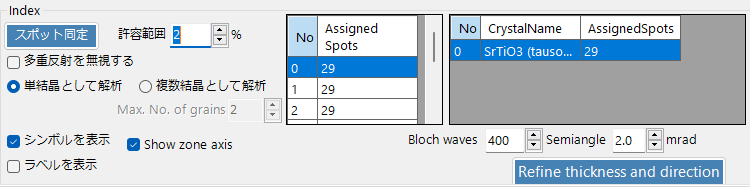
スポットの検出が行われた状態で 「スポット同定」 ボタンを押すと、スポットの指数付けが行われます。メインウィンドウで選択されている結晶が対象です。
許容範囲
どれくらいの誤差を許容するかを設定します。
多重反射を無視する
チェックした場合、多重反射を無視して解析を行います。
単結晶として解析/複数結晶として解析
単一の結晶として指数付けを行うか、複数の結晶として指数付けを行うかを選択します。後者を選択した場合は、最大何個の結晶を考慮するかを指定します。
シンボルを表示
指数付けされたスポットのラベルおよびシンボルを、画像にオーバーラップして表示するかどうかを選択します。
Refine thickness and direction
ブロッホ波法による動力学回折効果を考慮して、検出された回折強度に最もよく一致する試料厚みおよび結晶方位を求めます。
- フィッティングには、以下のような関数を用いています。$$
f(x,y)=\frac{A}{\pi H_1H2}\left[ \frac{\eta}{2} \left( 1+c \left\{ \left( \frac{x’}{H_1} \right)^2 + \left( \frac{y’}{H_2} \right)^2 \right\} \right)^{-3/2} + (1-\eta)\ln 2 \exp \left( -\ln 2 \left\{ \left( \frac{x’}{H_1} \right)^2 + \left( \frac{y’}{H_2} \right)^2 \right\} \right) \right]\\
+B_0+x’ B_x + y’ B_y
$$ただし、$$
x’=(x-x_0)\cos\theta +(y-y_0)\sin\theta, \,\,\, y’=(y-y_0)\cos\theta – (x-x_0)\sin\theta, \,\,\, c=4^{1/3}-1
$$ です。
角括弧(\([\,]\))内の第1項 \( \frac{1}{2} \left( 1+ \left\{ \left( \frac{x’}{H_1} \right)^2 +c \left( \frac{y’}{H_2} \right)^2 \right\} \right)^{-3/2} \) は2次元コーシー分布関数です。また、第2項 \(\ln 2 \exp \left( -\ln 2 \left\{ \left( \frac{x’}{H_1} \right)^2 + \left( \frac{y’}{H_2} \right)^2 \right\} \right) \) は2次元ガウス関数です。\(x_0, y_0\) はスポットの中心座標、 \(\theta\) は \(x,y\) 軸を \(x’,y’\) 軸に回転する角度、 \(H_1,H_2\) は \(x’,y’\) 軸に対する半値幅、 \(\eta\) はコーシー分布関数とガウス関数の比率を意味します。 \(A\) はこの関数の積分強度に対応します。また、後半の \(B_0+x’ B_x + y’ B_y\) の部分はバックグラウンド平面を意味しています。
フィッティングの際には、修正マルカート法を用いて逐次近似的に各パラメータを最適化します。 ↩︎