A.1.1. 全体の座標系 (回折シミュレータ機能を除く)
軸の定義 (Definition of orientation)
ReciProでは、様々な”方向”を取り扱いますので、その定義を説明します。
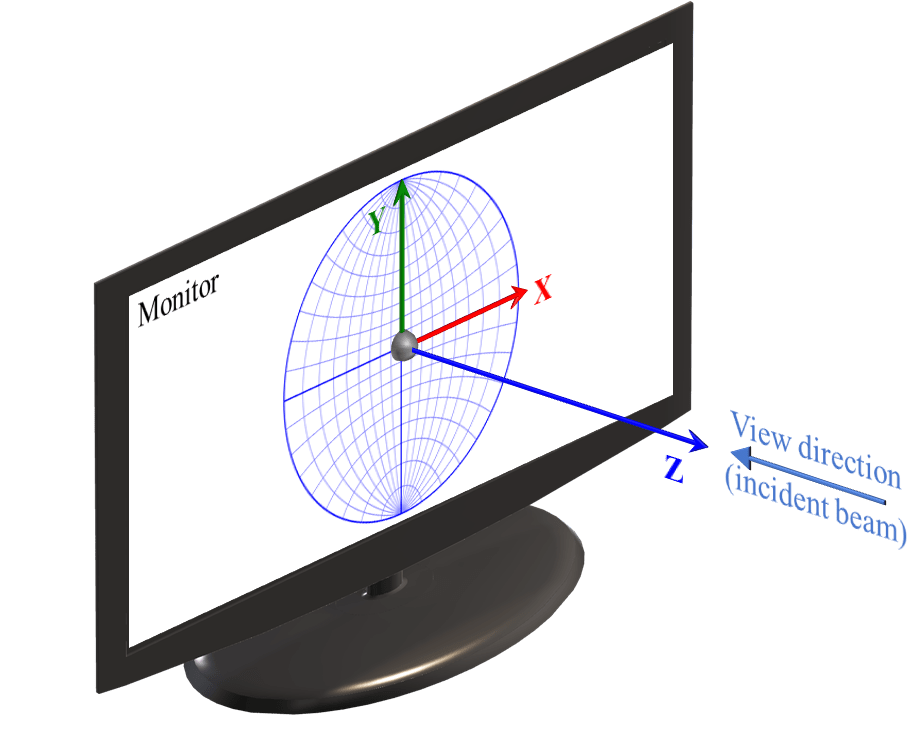
ReciProはこの図のように、
- X軸はモニター面の右方向
- Y軸はモニター面の上方向
- Z軸はモニター面の垂直手前方向
という右手系座標系を採用しています。
ビーム (Incident beam) の方向とモニターを見つめる視線の方向 (View direction) は一致しており、-Z軸に対応します。
ReciProで行う演算のほとんどは、方向 (すなわち3×3の回転行列) だけが意味を持ち、原点の位置を意識する必要はありません。ただし、「回折シミュレータ」 ウィンドウでは、原点位置を明確に考慮する必要があります。これについては A.1.2.をご覧ください。
初期の結晶方位 (Initial crystal direction)
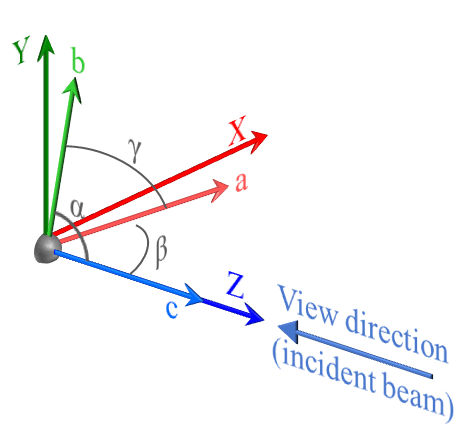
オイラー角 (Euler angles)
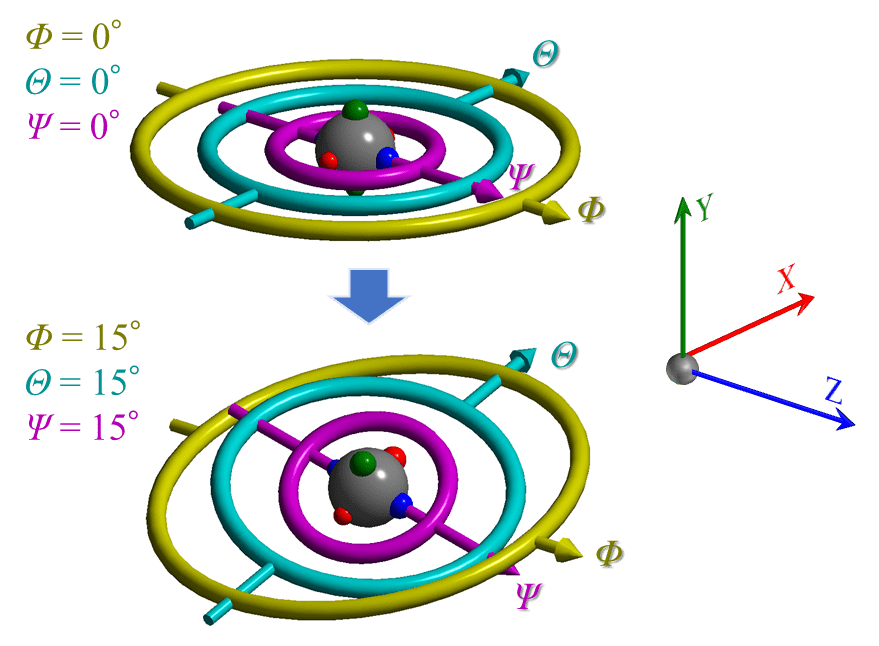
ReciProでは結晶を様々な方向に回転させることが出来ます。その結晶方位を表現するのがオイラー角 (Euler angles)です。
ReciProにおけるEuler anglesは図のようにΦ, θ, Ψという3つの記号を使います。上の図の上の方に示したように、角度Φ, θ, Ψがすべてゼロの時、それらの角度が相当する回転軸の方向は、それぞれZ, X, Zと一致します3。
3つのオイラー角には主従関係があることに注意してください。Φは最も上位(1st )の回転であり、θがそれに続きます(2nd )。Ψは最も下位(3rd )の回転です。下位の回転軸の方向は、上位の回転の状態によって変化します4。例として、上の図の下の方に、Φ, θ, Ψを全て15°にした状態を示しました。角度Φに相当する回転軸は常にZ軸と一致しますが、角度θと角度Ψに相当する回転軸は、一般的にX, Y, Zのどれとも一致しません。
A.1.2. 回折シミュレータウィンドウにおける座標系の定義
回折シミュレータでは検出器平面に写る回折パターンをシミュレーションしてモニターに表示します。検出器はピクセルの集合体が作る有限の大きさの平面であり、試料 (散乱体) から一定の距離に置かれています。さらにこの検出器は入射ビームに対して傾いているかもしれません。このような状況を正確にシミュレーションするために、検出器と試料との間の幾何学的関係や、検出器のピクセルサイズ・ピクセル数といった情報が重要になります。
検出器が傾いていない状態
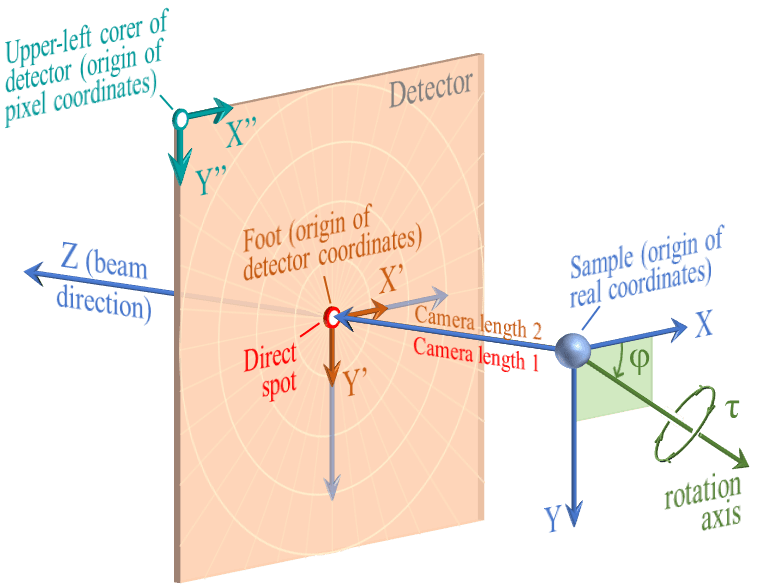
まず、この図のように、検出器が傾いていない(入射ビームと検出器平面の法線が一致する)状態を考えます。
ビームが検出器と交わる点をダイレクトスポット (Direct spot) とよび、試料からダイレクトスポットまでの距離をカメラ長1 (Camera length 1, C1)と定義します。一方、試料から検出器におろした垂線の足 (the foot of the perpendicular from the sample, Foot) までの距離はカメラ長2 (Camera length 2, C2) と定義します。検出器が傾いていない場合は、ダイレクトスポットと垂線の足は一致し、カメラ長1とカメラ長2 も等しい長さになります。
実空間座標 (Real coordinates) は 試料 (sample) を原点とする三次元直交座標系であり、単位は mm です。Z軸はビーム方向 (Beam direction) と必ず一致します (A.1.の定義と異なることに注意5)。X 軸方向は、Z 軸方向を正面に見て右向であり、Y 軸の方向は下向です。
検出器座標系 (Detector coordinates) は 垂線の足 (Foot)を原点とする二次元座標系であり、単位は mmです。検出器平面の右方向がX’軸、下方向がY’軸です。
ピクセル座標系 (Pixel coordinates) は検出器の左上の点を原点とする二次元座標系であり、単位はピクセルです。検出器座標系と同じく検出器平面の右方向がX’’軸、下方向がY’’軸です。
検出器が傾いている状態
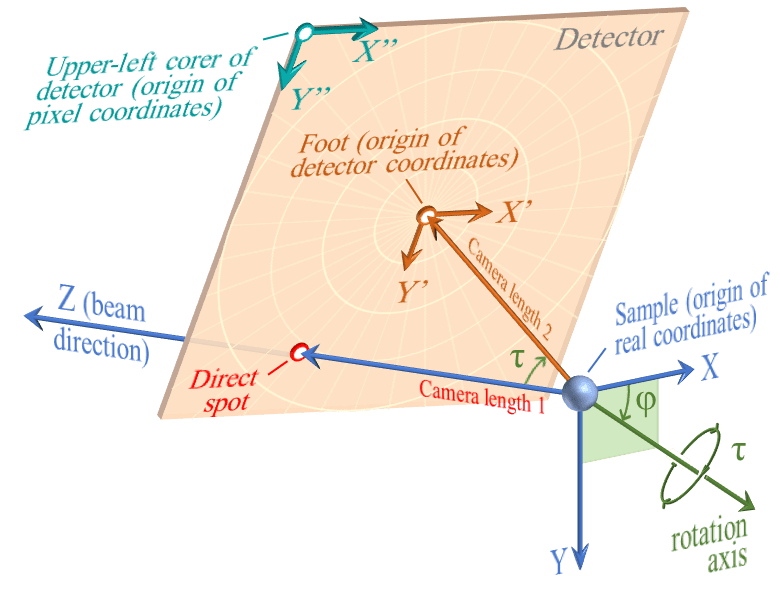
次に、検出器が傾いた状態を考えます。
検出器の傾きを表現するために、回転軸の方向 (φ) と回転量 (τ) という二つのパラメータを導入します。回転軸は XY 平面 (Z=0 平面) 上にあると考えて、X 軸からの角度を φ とします。そして、 φ によって定義される回転軸 (rotation axis) の周りに、右ネジの方向で τ だけ回転させる操作を行います。
φ と τ で定義される回転操作によって検出器が傾いた結果、ダイレクトスポットと垂線の足は一致しない状態になります6。繰り返しになりますが、前者と試料の距離をカメラ長1 (C1)、後者と試料の距離はカメラ長2 (C2)と定義しています7。検出器座標系の原点は常に「垂線の足」であり、ピクセル座標系の原点は常に検出器の左上の点であることに注意してください。また、検出器が傾くとX, Yの方向とX’, Y’の方向は一致しないことにも注意してください。
なお、検出器が傾いていても、ReciProの回折シミュレータはあくまで検出器平面を表示します。つまり、モニター見つめる方向と入射ビームの方向は一致しません。混乱しやすいポイントなのでご注意ください。
パラメータの意味・定義
以下に、各パラメータの意味・定義を改めて列記します。
実空間座標系 (Real coordinates) (X, Y, Z)
実験室空間における3次元直交座標系であり、単位は mm です。原点は常に試料 (sample) であり、Z軸はかならず入射ビームと方向も含めて一致します。もし検出器が傾いなければ (入射ビームと検出器平面が直交すれば)、 X 軸と Y 軸は後述する検出器座標系の X’ 軸と Y’ 軸の方向と平行になります。
試料 (Sample)
入射ビームによって散乱される物質のことです。サイズは無限小であると考え、実空間座標系の原点となります。
検出器の回転 (Rotation of detector)
検出器の回転状態は、Φとτで定義される回転操作によって定義されます。この回転軸は実空間座標系の原点(すなわち試料)を通り、XY平面上に位置しています。
φ
X軸と回転軸との間の角度です。ゼロの場合はX軸と一致します。角度の正方向は、Z軸方向に進む右ネジの回転方向です。
τ
回転量を示します。右ネジの方向です。
検出器座標系 (Detector coordinates) (X’, Y’)
検出器平面上の二次元直交座標系で、単位は mm です。この座標系の原点は垂線の足です。検出器に向かって右方向がX’軸、下方向がY’軸と定義します。検出器が傾いていない場合、X’ 軸と Y’軸は実空間座標系 X軸とY軸の方向と一致します。 また、後述するピクセル座標系の X”軸とY”軸とは常に平行です。
垂線の足 (Foot)
試料から検出器平面におろした垂線の足の位置です。検出器座標系の原点となります。もし検出器が傾いていなかったら、ダイレクトスポットの位置と一致します。
カメラ長2 (Camera length 2) (C2)
試料から垂線の足までの距離です。単位は mm です。
ダイレクトスポット (Direct spot)
試料を通った入射ビームが検出器と交わった点の位置です。単位は mm です。
カメラ長2 (Camera length 1) (C1)
試料からダイレクトスポットのまでの距離です。単位は mm です。
ピクセル座標系 (Pixel coordinates) (X’’, Y’’)
検出器平面上の二次元直交座標系で、単位は pixel です。検出器に向かって右方向が X” 軸、下方向が Y” 軸です。原点は常に検出器の左上です。
ピクセルサイズ (Pixel size)
ピクセルの一辺の長さです。単位は mm です。正方形の形状のみ対応しています。
検出器の幅/高さ (Detector width/height)
検出器のサイズ (幅と高さ)です。ピクセル単位です。
脚注
- この定義は、Oxford社のEBSDソフトのインターフェースと互換性を取るためです。 ↩︎
- cubic, tetragonal, or orthogonalの時、a, b, c軸の初期方位はそれぞれX, Y, Z軸と一致します。hexagonal, trigonal, or monoclinicの時、b, c軸はそれぞれY, Z軸と一致しますが、a軸はX軸と一致しません。triclinicの時、c軸はZ軸と一致しますが、a, b軸はX,Y軸と一致しません。 ↩︎
- Euler anglesの定義についても、Oxford社のEBSDソフトのインターフェースと互換性があります。 ↩︎
- 線形代数的な表現では、最終的な回転状態を \(R\) (3×3行列)としたとき、 \(R\) は以下のように計算できます。$$
R=
\begin{pmatrix}
\cos\Phi & -\sin\Phi&0\\
\sin\Phi & \cos\Phi&0\\
0 & 0&1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0\\
0 & \cos\theta & -\sin\theta\\
0 & \sin\theta&\cos\theta
\end{pmatrix}
\begin{pmatrix}
\cos\Psi & -\sin\Psi&0\\
\sin\Psi & \cos\Psi&0\\
0 & 0&1
\end{pmatrix}$$ ↩︎ - A.1.1. では ビーム方向を-Z方向と定義しましたが、「回折シミュレータ」 ウィンドウ ではビーム方向を+Zと定義します。それに付随して、Y軸の方向も反転します。これは、過去の文献や他のソフトとの整合性を担保するためです。また、一般的にコンピュータで画像を取り扱う際には画像の下方向を+Y方向として表現するのが普通であるという事情もあります。ただし、ユーザーサイドではこのような座標系の違いを意識する必要はありません。ReciProの内部で自動的に適切な座標系変換を行っています。 ↩︎
- 検出器座標系における垂線の足の座標 \((F_x, F_y)\)とダイレクトスポットの座標 \((D_x, D_y)\) は、次の関係があります。$$(D_x, D_y) = (F_x – C_2 \sin\phi \tan\tau , F_y + C_2 \cos\phi \tan\tau)$$なお\(C_2\)はカメラ長2 です。 ↩︎
- カメラ長1 (C1)とカメラ長 2 (C2)の関係は$$
C_1 \cos\tau = C_2
$$です。 ↩︎