3次元において半径が \(r\) の球の面積は \(4\pi r^2\) であることは誰でもご存じと思います。それでは、キャップ1 (spherical cap) の面積、あるいは、キャップとキャップが重なった部分の面積の求め方はご存じでしょうか?ここではこのような球の面積に関する少し高度な話題を取り上げます。
キャップの面積
キャップとは、球がある平面で切断されたときにできるお椀のような形状をした立体のことです。次の図のように、半径 \(r\) の球が、原点から \(r-h\) だけ離れた平面によって切られ、底面の半径が\(a\)、 高さが \(h\) 、開き角が \(\theta\) のキャップ(青色)に分かたれたとします。このキャップの面積を求めてみましょう。
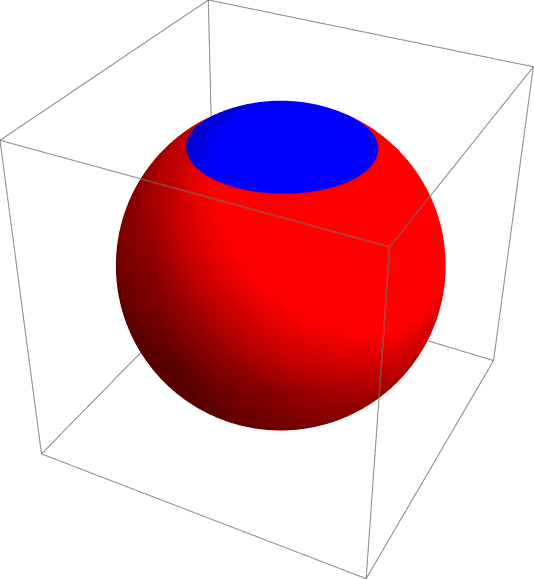

このキャップの表面積\(A\)は中心からの角度で積分すれば$$A=\int_0^\theta {2 \pi r^2 \sin\phi\ d\phi} = 2\pi r^2 (1-\cos\theta) $$となります2。\(r (1-\cos\theta)=h\) なので \(A=2\pi r h\) と書くこともできますし、\(r^2=a^2+(r-h)^2 \leftrightarrow 2rh=a^2+h^2\) なので \(A=\pi (a^2+h^2)\) と書くこともできます。
キャップとキャップの重なり面積
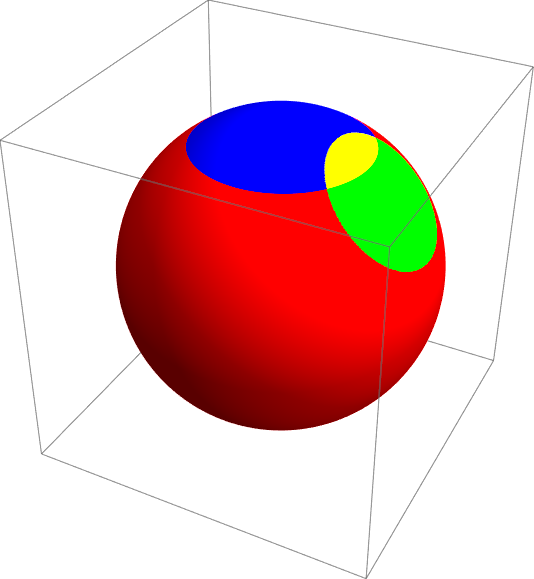
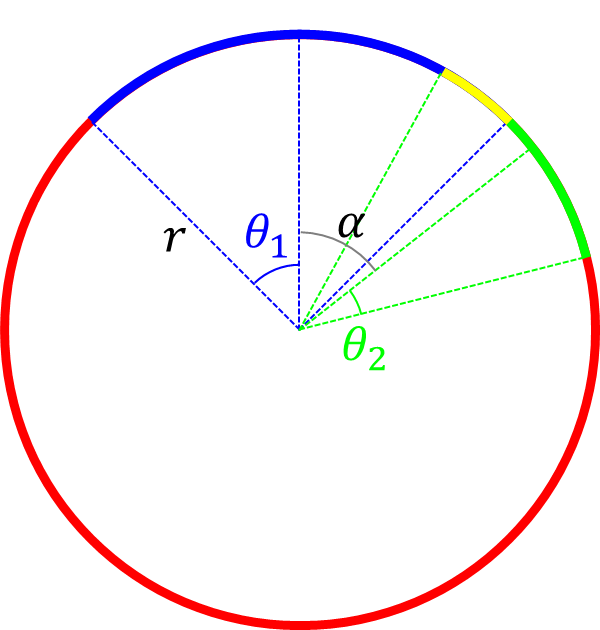
次はキャップとキャップが重なった部分の面積を考えてみましょう。劇的に難しくなります。次のような図3の状況を考え見ましょう。青のキャップと緑のキャップがあって、その重なり部分である黄色の面積を求めたいという問題です。青と緑のキャップの開き角がそれぞれ \(\theta_1、\theta_2\)でありキャップの中心がなす角は \(\alpha\)です。
- 球冠ということもあります。 ↩︎
- \(\phi \sim \phi+d\phi\) の環上のバンドは、長さが \(2\pi r \sin\phi\) で幅が\(r d\phi\) なので。 ↩︎
- r = 1.2;
sphere =ParametricPlot3D[r {Sin[th] Cos[ph], Sin[th] Sin[ph], Cos[th]}, {th, 0, Pi}, {ph, 0,2 Pi}, Mesh -> None,
ColorFunction ->Function[{x, y, z, th, ph},Which[z < 1 && (x + z)/Sqrt[2 (x^2 + y^2 + z^2)] < 0.9, Red, z > 1 && (x + z)/Sqrt[2 (x^2 + y^2 + z^2)] > 0.9, Yellow,z > 1 , Blue, True, Green]],ColorFunctionScaling -> False, PlotPoints -> {800, 800},MaxRecursion -> 2, PerformanceGoal -> “Quality”,PlotRange -> All];
Show[sphere, PlotRange -> All, Boxed -> True, Axes -> False,ImageSize -> 400] ↩︎